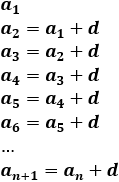Progresión aritmética

Una sucesión (o progresión) es un conjunto de números ordenados. Cada número ocupa una posición y recibe el nombre de término.

Ejemplos:

  • Sucesión de los números pares: 2, 4, 6, 8, 10, 12, 14,…
  • Sucesión de los números impares: 1, 3, 5, 7, 9, 11, 13,…
  • Sucesión de los naturales: 1, 2, 3, 4, 5, 6,…

El primer término de una sucesión se denota por a1, el segundo por a2, el tercero por a3 y así sucesivamente.

Una sucesión es aritmética cuando cada término se calcula sumando un número d al término anterior:

En la sucesión de los números pares, la diferencia es d = 2.

Diferencia

La diferencia de una sucesión aritmética se calcula restando términos consecutivos:

Ejemplos:

  • La diferencia de la sucesión de los números pares es d = 2.
  • La diferencia de la sucesión de los números impares es d = 2.
  • La diferencia de la sucesión de los números naturales es d = 1.

Término general

El término general de una sucesión es la fórmula que permite calcular cualquier término de la sucesión.

Ejemplos: 

  • El término general de la sucesión de los números pares es an = 2·n. Para calcular, por ejemplo, el cuarto término de la sucesión, sustituimos n por 4 en la fórmula: a4 = 2·4 = 8.
  • El término general de la sucesión de los números impares es an = 2·n – 1. Para calcular, por ejemplo, el cuarto término de la sucesión, sustituimos n por 4 en la fórmula: a4 = 2·4 – 1 = 7.
  • El término general de la sucesión de los números naturales es an = n. 

 

El término general an se calcula a partir de la diferencia d y del primer término a1:

Recursos de sucesiones (ejemplos y problemas resueltos):