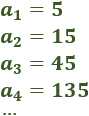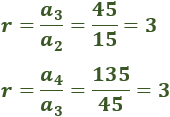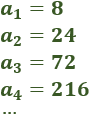Una sucesión geométrica (o progresión geométrica) es una sucesión en la que cada término an se obtiene multiplicando al término anterior an-1 por un número r llamado razón.
Ejemplos:
- La sucesión 2, 4, 8, 16, 32,… es geométrica con razón r = 2:
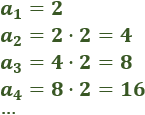
- La sucesión 1, -3, 9, -27, 81,… es geométrica con razón r = -3.
Razón
La razón se calcula dividiendo términos consecutivos:
Ejemplo:
Calculamos la razón de la siguiente sucesión geométrica:
Dividimos el segundo término entre el primero:
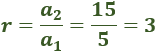
Comprobamos que la razón es constante:
Término general
El término general de una sucesión geométrica se calcula a partir del primer término a1 y de la razón r:
![]()
El término general permite calcular cualquier término de la sucesión sin necesidad de calcular los anteriores.
Ejemplo:
Calculamos el término general de la siguiente progresión geométrica:
La razón de la sucesión es r=3 ya que
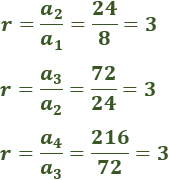
El término general de la sucesión es
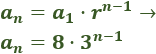
Suma de términos
Para sumar los primeros n términos de una progresión geométrica disponemos de varias fórmulas:
Primera fórmula:
Segunda fórmula:
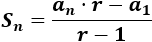
Nota: la segunda fórmula se ha calculado utilizando la fórmula del término general en la primera fórmula de la suma.
Suma de todos los términos
Cuando la razón de la progresión es |r|<1 se pueden sumar todos los términos mediante la fórmula
Recursos de sucesiones (ejemplos y problemas resueltos):
- Test básico de progresiones
- Tipos de progresiones
- Progresiones aritméticas
- Progresiones geométricas
- Problemas de progresiones aritméticas y geométricas
- La sucesión de Fibonacci
- Calculadoras de progresiones aritméticas
- Calculadoras de progresiones geométricas
- Operaciones entre sucesiones
- Límites de sucesiones
- Subsucesiones o sucesiones parciales
- Introducción a las progresiones
- Criterio de la media aritmética
- Criterios de la media geométrica y de la raíz
- Criterio de Stolz
- Sucesiones