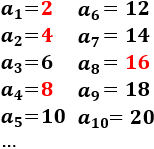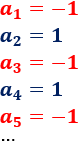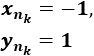1. Definición

De forma no rigurosa, una subsucesión de la sucesión a(n) es una sucesión que está dentro de la sucesión a(n).

Ejemplo: La sucesión de los números pares es a(n)=2n. Una subsucesión de a(n) es la sucesión de las potencias de dos: b(n) = 2ⁿ.

Los primeros términos de a(n) son

En rojo hemos indicado las potencias de 2, que son los términos de la subsucesión b(n).

Los primeros términos de b(n) son

b(1) = 2 = a(1)

b(2) = 2² = 4 = a(2)

b(3) = 2³ = 8 = a(4)

b(4) = 2⁴ = 16 = a(8)

b(5) = 2⁵ = 32 = a(16)

…

b(n) = 2ⁿ = a(2^n-1)

Nota: las subsucesiones de a(n) deben estar compuestas por infinitos términos de a(n). Por ejemplo, la sucesión constante c(n) = 2 = a(1) no es una subsucesión de a(n) porque sólo está formada por un término de a(n).

2. Propiedades

• Sea a(n) una sucesión convergente a L≠∞, entonces todas sus subsucesiones convergen a L.
• Sea a(n) una sucesión acotada, entonces todas sus subsucesiones son acotadas.
• Si una sucesión a(n) tiene dos subsucesiones que convergen a límites distintos, entonces la sucesión a(n) no converge.
• Teorema de Bolzano-Weierstrass: Sea a(n) una sucesión acotada, entonces tiene alguna subsucesión convergente.

3. Ejemplos

Problema 1: Sea la sucesión alternada dada por

Demostrar que no converge a partir de sus subsucesiones.

Solución:

La sucesión es alternada y sus primeros términos son

Sean las subsucesiones

Son sucesiones convergentes porque son constantes, pero sus límites son distintos. Por tanto, a(n) no converge.

Problema 2: Sea la sucesión alternada dada por

Calcular el límite de las siguientes subsucesiones de a(n):

• x(n) = a(2n)
• y(n) = a(2n+1)
• z(n) = a(n^2)

 

Solución:

 

La sucesión a(n) es alternada, pero es convergente a 0 ya que la fracción tiende a 0:

Los términos de a(n) van cambiando de signo, pero aproximándose a 0. Como consecuencia de la convergencia de a(n), todas las subsucesiones de a(n) convergen también a 0.