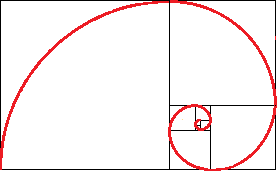
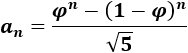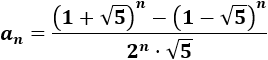La sucesión de Fibonacci es conocida desde hace miles de años, pero fue Fibonacci (Leonardo de Pisa) quien la dio a conocer al utilizarla para resolver un problema.
La sucesión
El primer y segundo término de la sucesión son
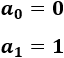
Los siguientes términos se obtienen sumando los dos términos que les preceden:
El tercer término de la sucesión es
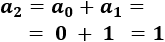
El cuarto término es
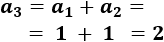
El quinto término es
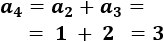
El sexto término es
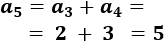
Y así, sucesivamente.
Por tanto, el término de la posición n+1 es
![]()
Fórmula de Binet
La sucesión de Fibonacci está definida por recurrencia. Esto significa que para calcular un término de la sucesión se necesitan los términos que le preceden. Esto es, a priori, un problema a la hora de calcular términos de posiciones muy altas.
Este problema se resuelve mediante la llamada fórmula de Binet:
Operando un poco,
Sin embargo, este término general también presenta un inconveniente: las potencias enésimas de binomios y raíces.
El número de oro
El número áureo o el número de oro es el número irracional
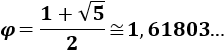
Su relación con la sucesión de Fibonacci es que es el límite de los cocientes de sus términos:
Esto significa que los cocientes de los términos consecutivos de la sucesión de Fibonacci se aproximan al número áureo.
Más información: propiedades de la sucesión de Fibonacci y problemas resueltos.
Recursos de sucesiones:
- Test básico de progresiones
- Tipos de progresiones
- Progresiones aritméticas
- Progresiones geométricas
- Problemas de progresiones aritméticas y geométricas
- Calculadoras de progresiones aritméticas
- Calculadoras de progresiones geométricas
- Operaciones entre sucesiones
- Límites de sucesiones
- Subsucesiones o sucesiones parciales
- Introducción a las progresiones
- Criterio de la media aritmética
- Criterios de la media geométrica y de la raíz
- Criterio de Stolz
- Sucesiones