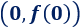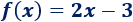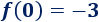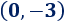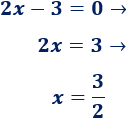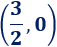Una función lineal es una función polinómica de primer grado. Es decir, tiene la siguiente forma
siendo m ≠ 0.
- m es la pendiente de la función
- n es la ordenada (en el origen) de la función
La gráfica de una función lineal es siempre una recta.
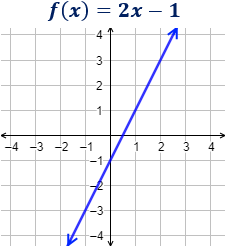
Ejemplo:
La pendiente de la función es m = 2 y la ordenada es n = -1.
La pendiente es el coeficiente de la variable, es decir, m.
Geométricamente, cuanto mayor es la pendiente, más inclinada es la recta. Es decir, más rápido crece la función.
- Si la pendiente es positiva, la función es creciente.
- Si la pendiente es negativa, la función es decreciente.
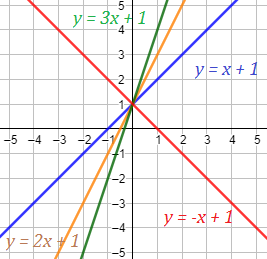
Ejemplo:
Rectas con pendientes 1, 2, 3 y -1:
Observad que la recta con pendiente negativa -1 es decreciente (la roja). Las otras tres rectas son crecientes.
De las rectas crecientes, la que crece más rápidamente es la verde (pendiente 3).
Puntos de corte
El punto de corte con el eje Y es el punto de la recta que tiene la primera coordenada igual a 0:
El punto de corte con el eje X es el punto de la recta que tiene 0 en la segunda coordenada. Se calcula igualando a 0 la función y resolviendo la ecuación obtenida.
Ejemplo
Calculamos los puntos de corte de la función del ejemplo anterior,
Corte con el eje Y:
Es el punto
Observad que la segunda coordenada es la ordenada.
Corte con el eje X:
Es el punto
Problemas relacionados: