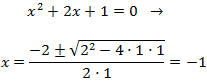La regla de Ruffini es un método (algoritmo) que nos permite obtener las raíces de un polinomio. Es de gran utilidad ya que para grado mayor que 2 no disponemos de fórmulas, al menos fáciles, para poder obtenerlas.
Cada vez que hacemos una tabla a partir de los coeficientes del polinomio, obtenemos una raíz y los coeficientes de un polinomio de un grado menor (un polinomio que divide al propio polinomio). De este modo, podemos ir reduciendo el grado del polinomio hasta llegar a uno de segundo grado cuyas raíces sabemos calcular rápidamente.
En realidad, el método consiste escoger una posible raíz y desarrollar una tabla. Si el último resultado de la tabla es 0, el procedimiento habrá finalizado correctamente. Si no es así, tendremos que probar con otra posible raíz.
Toda raíz ha de ser un divisor del término independiente (el término del polinomio que no tiene parte literal, es decir, que no tiene x).
Vamos a explicar el método a través de un ejemplo.
Ejemplo
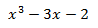
El polinomio es de grado 3.
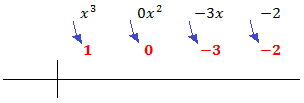
Escribimos en la primera fila los coeficientes de cada monomio en orden decreciente de grado. Si hay algún coeficiente que sea 0 (en nuestro caso es el coeficiente de x 2 ), también hay que escribirlo.
Ahora buscamos un número que sea divisor del término independiente, es decir, del término que no tiene parte literal (ninguna x), y lo escribimos en la columna de la izquierda.
En nuestro polinomio el independiente es -2. Podemos escoger 1, -1, 2 ó -2. Escogemos, por ejemplo, 2, que es divisor de -2 y tiene el signo contrario. Si no funciona, tendremos que probar con otro hasta dar con el bueno.
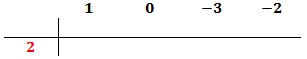
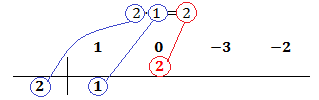
El primer coeficiente pasa a la parte inferior de la línea, sin realizar ninguna operación.
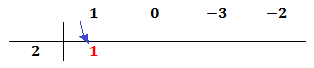
Ahora multiplicamos el coeficiente que hemos bajado por el número de la columna izquierda y el resultado lo escribimos debajo del siguiente coeficiente, pero arriba de la línea.
Sumamos el número que hemos escrito con el coeficiente que tiene arriba y el resultado lo escribimos debajo de la línea:
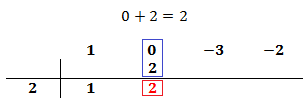
Ahora repetimos el proceso:
Multiplicamos el número obtenido por el de la columna izquierda y lo situamos debajo del siguiente coeficiente:
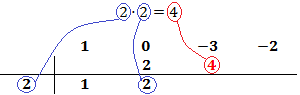
Sumamos el número que hemos escrito con el coeficiente que tiene arriba y el resultado lo escribimos debajo de la línea:
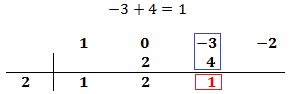
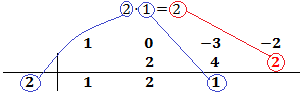
Multiplicamos el número obtenido por el de la columna izquierda y lo situamos debajo del siguiente coeficiente:
Sumamos el número que hemos escrito con el coeficiente que tiene arriba y el resultado lo escribimos debajo de la línea:
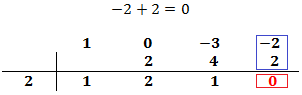
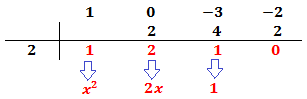
Es importante que el último número del proceso sea 0. Si no es así, significa que el número de la columna izquierda no nos sirve y debemos escoger otro.
La raíz que del polinomio que hemos calculado está en la columna izquierda.
Tenemos la raíz x = 2.
Los números de debajo de la línea son los coeficientes de un polinomio de un grado menos (en nuestro caso, de grado 2).
El polinomio de un grado menor es
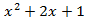
Por tanto, la primera factorización es
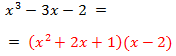
Y la raíz x = 2.
Si queremos calcular las otras raíces, aplicamos de nuevo el método al polinomio de un grado menos. En nuestro caso, como es de grado 2, usamos la fórmula para las ecuaciones cuadráticas:
Es una raíz doble.
Recursos:
- Más ejemplos de la regla de Ruffini
- Multiplicar polinomios
- Propiedades de las ecuaciones de segundo grado
- Resolución de ecuaciones cuadráticas incompletas
- Resolución de ecuaciones cuadráticas completas
- Ecuaciones cuadráticas con soluciones complejas
- Ecuaciones de segundo grado completas e incompletas
- Ecuaciones bicuadradas
Ecuaciones cuadráticas por niveles: