Conjugado de un número imaginario

Dado un número complejo en su forma binómica z=a+bi, se define su conjugado como

Definición de módulo, argumento y conjugado de los números complejos, con interpretación geométrica y ejemplos. Enunciamos las propiedades básicas del conjugado y del módulo (de la suma, del producto, del cociente, etc.). Matemáticas. Números complejos. Secundaria. Bachillerato. Universidad.

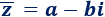
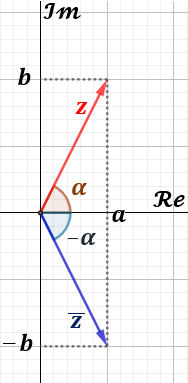
Si representamos un complejo y su conjugado, son simétricos respecto del eje horizontal:

Definición de módulo, argumento y conjugado de los números complejos, con interpretación geométrica y ejemplos. Enunciamos las propiedades básicas del conjugado y del módulo (de la suma, del producto, del cociente, etc.). Matemáticas. Números complejos. Secundaria. Bachillerato. Universidad.

Tened en cuenta que la longitud de los vectores es la misma (tienen el mismo módulo) y los argumentos son iguales porque la arcotangente es una función impar:

Definición de módulo, argumento y conjugado de los números complejos, con interpretación geométrica y ejemplos. Enunciamos las propiedades básicas del conjugado y del módulo (de la suma, del producto, del cociente, etc.). Matemáticas. Números complejos. Secundaria. Bachillerato. Universidad.

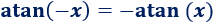
Ejemplos:

  • El conjugado de 1+3i es 1-3i.
  • El conjugado de 2-i es 2+i.
  • El conjugado de 5 es 5.
  • El conjugado de 3i es -3i.
  • El conjugado de -1+2i es -1-2i.

Algunas propiedades:

Conjugado del conjugado:

Definición de módulo, argumento y conjugado de los números complejos, con interpretación geométrica y ejemplos. Enunciamos las propiedades básicas del conjugado y del módulo (de la suma, del producto, del cociente, etc.). Matemáticas. Números complejos. Secundaria. Bachillerato. Universidad.

Conjugado de la suma:

Definición de módulo, argumento y conjugado de los números complejos, con interpretación geométrica y ejemplos. Enunciamos las propiedades básicas del conjugado y del módulo (de la suma, del producto, del cociente, etc.). Matemáticas. Números complejos. Secundaria. Bachillerato. Universidad.

Conjugado del producto de complejos:

Definición de módulo, argumento y conjugado de los números complejos, con interpretación geométrica y ejemplos. Enunciamos las propiedades básicas del conjugado y del módulo (de la suma, del producto, del cociente, etc.). Matemáticas. Números complejos. Secundaria. Bachillerato. Universidad.

Producto de un complejo por su conjugado:

Definición de módulo, argumento y conjugado de los números complejos, con interpretación geométrica y ejemplos. Enunciamos las propiedades básicas del conjugado y del módulo (de la suma, del producto, del cociente, etc.). Matemáticas. Números complejos. Secundaria. Bachillerato. Universidad.

Conjugado del cociente de complejos:

Definición de módulo, argumento y conjugado de los números complejos, con interpretación geométrica y ejemplos. Enunciamos las propiedades básicas del conjugado y del módulo (de la suma, del producto, del cociente, etc.). Matemáticas. Números complejos. Secundaria. Bachillerato. Universidad.

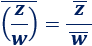
Suma de un complejo con su conjugado:

Definición de módulo, argumento y conjugado de los números complejos, con interpretación geométrica y ejemplos. Enunciamos las propiedades básicas del conjugado y del módulo (de la suma, del producto, del cociente, etc.). Matemáticas. Números complejos. Secundaria. Bachillerato. Universidad.

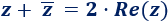
Resta de un complejo con su conjugado:

Definición de módulo, argumento y conjugado de los números complejos, con interpretación geométrica y ejemplos. Enunciamos las propiedades básicas del conjugado y del módulo (de la suma, del producto, del cociente, etc.). Matemáticas. Números complejos. Secundaria. Bachillerato. Universidad.

Módulo del conjugado:

Definición de módulo, argumento y conjugado de los números complejos, con interpretación geométrica y ejemplos. Enunciamos las propiedades básicas del conjugado y del módulo (de la suma, del producto, del cociente, etc.). Matemáticas. Números complejos. Secundaria. Bachillerato. Universidad.

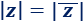
Más información: