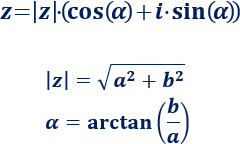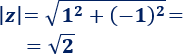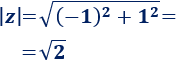Forma binómica, trigonométrica y polar de números imaginarios

En la forma binómica, un complejo  se escribe como la suma de un número real  y un número real  multiplicado por la unidad imaginaria :

El número  es la parte real de  y  es la parte imaginaria de .

 

La forma trigonométrica del complejo $z=a+bi$ es

El ángulo α que proporciona la función arcotangente es siempre entre -45° y 45°. Si el complejo pertenece el primer cuadrante ($a>0$, $b>0$) o al cuarto ($a>0$, $b<0$), el ángulo obtenido es el argumento del complejo.

Sin embargo, si el complejo está en el segundo cuadrante ($a<0$, $b>0$), hay que sumarle 180°. Y si está en el tercer cuadrante, ($a<0$, $b<0$), hay que restarle 180°.

Hay una función proporciona directamente el argumento: $atan2(a,b)$.

$El\; módulo,$ es la raíz cuadrada de la suma del cuadrado de la parte real y de la parte imaginaria:

Ejemplo: escribimos el complejo z = 1-i en forma trigonométrica:

Calculamos el módulo:

Calculamos el ángulo que forma $\mathrm{z:}$

Por tanto, la forma trigonométrica de $z$ es

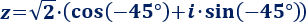
En la forma polar, el complejo se escribe en función de su módulo $|z|$ y su argumento $\alpha$como

Ejemplo: escribimos el número imaginario z = -1+i en forma polar

Calculamos el módulo del complejo :

Calculamos su argumento:

Nota: hemos sumado 180º grados al ángulo obtenido (-45º) porque el complejo está en el segundo cuadrante).

Por tanto, la forma polar de $z$ es

Más información:

• Introducción a los números complejos
• Formas binómica y polar
• Módulo y argumento de complejos
• Operaciones entre complejos
• Producto y cociente de complejos en forma binómica
• Producto y cociente de complejos en forma polar
• Propiedades de los números complejos
• Raíces de números complejos
• Calculadora de operaciones entre complejos
• Calculadora de forma polar y binómica de complejos
• Ecuaciones cuadráticas con soluciones complejas