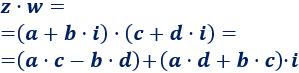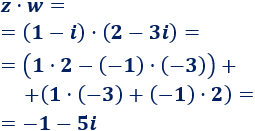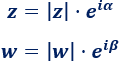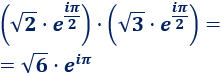En forma binómica
Sean z y w dos complejos dados en su forma binómica:
La multiplicación de los complejos z y w se define como
Nota: para obtener la fórmula, podéis calcular el producto como si fuera un producto de binomios, teniendo en cuenta que i2= -1.
Ejemplo: multiplicamos los números imaginarios 1-i y 2-3i:
En forma polar
Sean los números imaginarios z y w dados en su forma polar:
donde |z| y α son el módulo y el argumento de z y |w| y β son los de w.
Entonces, su producto es el complejo cuyo módulo es el producto de los módulos de los complejos y su argumento (ángulo) es la suma de sus argumentos.
Ejemplo:
Más información:
- Introducción a los números complejos
- Formas binómica y polar
- Módulo y argumento de complejos
- Operaciones entre complejos
- Producto y cociente de complejos en forma binómica
- Producto y cociente de complejos en forma polar
- Propiedades de los números complejos
- Raíces de números complejos
- Calculadora de operaciones entre complejos
- Calculadora de forma polar y binómica de complejos
- Ecuaciones cuadráticas con soluciones complejas