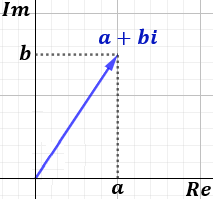
La forma habitual de representar a los números complejos es hacerlo como vectores del plano. Pero el plano se denomina, en este caso, plano complejo.
El complejo z = a+bi se representa como el vector con coordenadas (a, b):
- El eje horizontal es el eje real.
- El eje vertical es el eje imaginario.
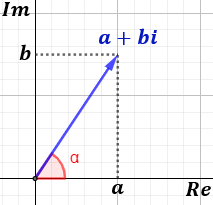
La longitud del vector se denomina módulo del complejo z y se representa por |z|.
El ángulo que forma el vector con la parte positiva del eje real se denomina argumento del complejo z:
Ejemplos:
Representación del complejo z = 1+2i:
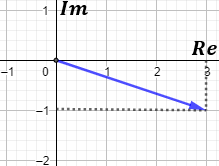
Representación del complejo w = 3-i:
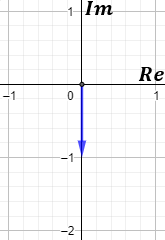
Representación del complejo q = -i:
Más información:
- Introducción a los números complejos
- Formas binómica y polar
- Módulo y argumento de complejos
- Operaciones entre complejos
- Producto y cociente de complejos en forma binómica
- Producto y cociente de complejos en forma polar
- Propiedades de los números complejos
- Raíces de números complejos
- Calculadora de operaciones entre complejos
- Calculadora de forma polar y binómica de complejos
- Ecuaciones cuadráticas con soluciones complejas