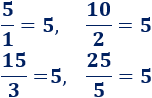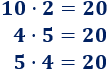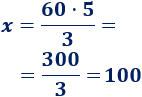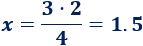Proporcionalidad simple y regla de tres

Veamos un par de ejemplos con los que entenderemos fácilmente qué es una relación de proporcionalidad. Después, explicamos cómo aplicar una regla de tres.

Proporcionalidad directa

En una fábrica de balones, cada trabajador fabrica 5 balones al día. Si la empresa contrata más trabajadores, el número de balones que se fabrica será mayor.

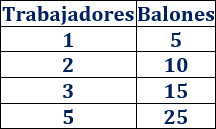
Escribimos una tabla con el número de trabajadores y el de balones fabricados al día:

Explicamos la relación de proporcionalidad simple directa e inversa y cómo aplicar una regla de tres, con ejemplos y problemas resueltos. ESO. Álgebra básica.

A medida que aumenta el número de trabajadores, lo hace el número de balones.

Estas dos magnitudes (número de trabajadores y de balones) mantienen una relación de proporcionalidad directa.

Si dividimos el número de balones entre el de trabajadores, obtenemos un resultado constante:

Explicamos la relación de proporcionalidad simple directa e inversa y cómo aplicar una regla de tres, con ejemplos y problemas resueltos. ESO. Álgebra básica.

Este número se denomina constante de proporcionalidad o razón.

Proporcionalidad inversa

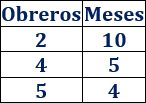
El tiempo que se tarda en construir una casa entre 2 obreros es 10 meses. Si el número de obreros aumenta, el tiempo que se tarda es menor.

Explicamos la relación de proporcionalidad simple directa e inversa y cómo aplicar una regla de tres, con ejemplos y problemas resueltos. ESO. Álgebra básica.

Estas dos magnitudes mantienen una relación de proporcionalidad inversa: cuando una magnitud aumenta, la otra disminuye y viceversa.

La constante de proporcionalidad se calcula multiplicando las magnitudes:

Explicamos la relación de proporcionalidad simple directa e inversa y cómo aplicar una regla de tres, con ejemplos y problemas resueltos. ESO. Álgebra básica.

Regla de tres

Existe una regla que nos permite calcular una de las magnitudes a partir de la otra. Esta regla se denomina regla de tres (directa o inversa).

Proporcionalidad directa

Nos ayudamos de un ejemplo.

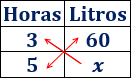
Si en 3 horas llueven 60 litros de agua, ¿cuántos lloverán en 5 horas?

Escribimos los tres datos en una tabla, cada magnitud en su columna correspondiente:

Explicamos la relación de proporcionalidad simple directa e inversa y cómo aplicar una regla de tres, con ejemplos y problemas resueltos. ESO. Álgebra básica.

Observad las flechas representadas en forma de cruz. Los datos de la flecha doble se multiplican y el resultado se divide entre el dato de la flecha simple:

Explicamos la relación de proporcionalidad simple directa e inversa y cómo aplicar una regla de tres, con ejemplos y problemas resueltos. ESO. Álgebra básica.

Lloverán 100 litros en 5 horas.

 

Proporcionalidad inversa

Nos ayudamos de un ejemplo.

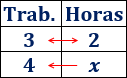
Si 3 trabajadores tardan 2 horas en cargar un camión, ¿cuánto tardarían en hacerlo 4 trabajadores?

Escribimos los tres datos en una tabla, cada magnitud en su columna correspondiente:

Explicamos la relación de proporcionalidad simple directa e inversa y cómo aplicar una regla de tres, con ejemplos y problemas resueltos. ESO. Álgebra básica.

Observad las flechas paralelas. Los datos de la flecha doble se multiplican y el resultado se divide entre el dato de la flecha simple:

Explicamos la relación de proporcionalidad simple directa e inversa y cómo aplicar una regla de tres, con ejemplos y problemas resueltos. ESO. Álgebra básica.

Dos obreros tardarían una hora y media.

 

Más ejemplos: