El sistema octal es un sistema de numeración posicional de base 8.
Los símbolos que se usan en este sistema son:
0, 1, 2, 3, 4, 5, 6, 7
Para indicar que un número está escrito en base 8, usamos el subíndice (8, y para indicar que un número está escrito en base 10, usamos el subíndice (10.
Ejemplos:
- 13(8 = 11(10
- 25(8 = 21(10
- 1077(8 = 575(10
A continuación, explicamos el método para pasar del sistema decimal al sistema octal mediante un ejemplo. Escribiremos el número 768(10 en base 8:
- Dividimos el número entre 8:
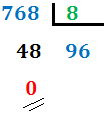
- Si el cociente es mayor o igual que 8, lo dividimos entre 8.En nuestro caso, el cociente es 96 (mayor que 8), por lo que lo dividimos de nuevo:
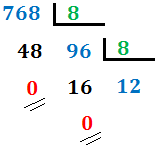
- Continuamos así hasta obtener un cociente menor que 8.En nuestro caso, el cociente es 12 (mayor que 8), así que lo dividimos de nuevo:
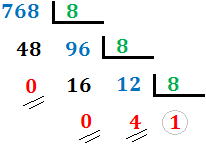
El cociente es 1, menor que 8, con lo que hemos terminado el proceso. Hemos indicado los restos con dos rayas y el último cociente con una circunferencia.
- El número en base 8 es:(Último cociente) (Último resto) (Penúltimo resto)… (Segundo resto) (Primer resto).
En nuestro caso,
- El último cociente es 1.
- El último resto es 4.
- El penúltimo resto es 0.
- El primer resto es 0.
Por tanto, el número 768 en base octal es 1400. Es decir,
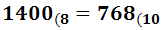
Recursos:
