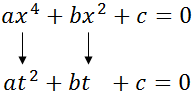En este post vamos a explicar cómo resolver ecuaciones bicuadradas mediante un cambio de variable. Es necesario saber resolver ecuaciones de segundo grado (completas e incompletas).
Una ecuación bicuadrada es una ecuación de cuarto grado con la forma
ax4 + bx2 + c = 0, a ≠ 0
Como es una ecuación de cuarto grado, puede tener hasta 4 soluciones. Para resolver este tipo de ecuaciones tenemos básicamente dos métodos:
- La regla de Ruffini
- Método de sustitución o cambio de variable.
En este post vamos a explicar el método de sustitución.
Método de sustitución
El método de sustitución que aplicamos puede resumirse en tres sencillos pasos:
1. Sustituimos x2 por t.
Al sustituir x2 por t, también tenemos que sustituir x4 por t2 porque
x4 = (x2)2 = t2
Al hacer este cambio, obtendremos una ecuación de segundo grado:
2. Resolvemos la ecuación de segundo grado
La solución de la ecuación de segundo grado tiene, como máximo, dos soluciones: t = t1 y t = t2.
3. Calculamos las soluciones (de la ecuación bicuadrada)
Como hemos aplicado el cambio t = x2, las soluciones son el cuadrado de las soluciones de la ecuación bicuadrada. Por tanto, para calcularlas, tenemos que hacer la raíz cuadrada:
x1 = + √t1 , x2 = – √t1
x3 = + √t2 , x4 = – √t2
Observad que de cada una de las soluciones t1 y t2 se obtiene 2 soluciones porque al hacer la raíz tenemos que escribir los dos signos + y – .
Ejemplos: ecuaciones bicuadradas resueltas.
Ecuaciones de segundo grado: