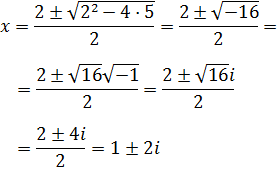Recordamos que la forma general de una ecuación cuadrática o de segundo grado es
donde a ≠ 0 , b y c los coeficientes.
El discriminante de la ecuación anterior es ![]()
El signo del discriminante informa acerca del número de soluciones de la ecuación:
- Si Δ es 0, la ecuación tiene una única solución real.
- Si Δ es menor que 0, existen dos soluciones complejas.
- Si Δ es mayor que 0, existen dos soluciones reales distintas.
Vamos a ver un ejemplo de ecuación con soluciones complejas (discriminante negativo).
Ejemplo:
El discriminante de la siguiente ecuación es -16:
Calculamos sus soluciones:
Por tanto, las soluciones de la ecuación son 1+2i y 1-2i.
Observad que las soluciones son números complejos conjugados.
Páginas con ecuaciones de segundo grado:
- Introducción a las ecuaciones de segundo grado
- Discriminante de la ecuación
- Ecuaciones incompletas resueltas
- Ecuaciones completas resueltas
- Ecuaciones con soluciones complejas
- Ecuaciones de segundo grado
- Ecuaciones incompletas resueltas (2)
- Ecuaciones completas resueltas (2)
- Propiedades de las ecuaciones cuadráticas
- Ecuaciones con soluciones complejas