Sesión correspondiente al día (14/12/2010).
CÁLCULO DE COMPONENTES CONEXAS
Diremos que una componente conexa (CC( asociada a un vértice vi es:
Conjunto de vértices a los que alcanza vi:
R(vi)
Y que alcanza a vi:
Q(vi)
CC asociada a vi: R(vi) ∩ Q(vi)
Una componente conexa asociada a un vértice “v” es un conjunto de vértices alcanzables por”v” y que a su vez pueden alcanzar a “v”.
Hay dos procedimientos o métodos para calcular las componentes conexas de un grafo:
Método 1 – Procedimiento del algoritmo
Sea G=(V, A) un grafo dirigido:
Etapa 1. Inicializar i<-1, V(1) = V
Etapa 2. Tomar vi E V(i)
Etapa 3. Calcular R(i) ∩ Q(vi)
-Hacer V(i+1) = V(i) ≈ R(vi) ∩ Q(vi)
-Hacer i<-i+1
Etapa 4. Si V(i) = ø entonces STOP
En otro caso, volvemos a la Etapa 2.
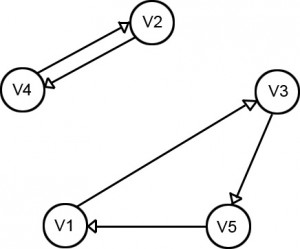
EJEMPLO
Vamos a calcular las componentes conexas del siguiente grafo, para ello necesitamos la matriz de accesibilidad y la matriz de acceso que es la traspuesta de la de accesibilidad:
Ahora sigamos el algoritmo paso a paso:
Debemos hacer dos conjuntos, R y Q.
Inicialmente cogemos todo el conjunto de vértices que tenemos y de ahí cogemos un vértice.
Una vez hecho vamos a la matriz de accesibilidad y buscamos la fila del vértice elegido, entonces vemos columna a columna si hay un uno o un cero, si hay un uno añadimos el vértice al conjunto R. Una vez hecho debemos hacer lo mismo para el conjunto Q pero mirando en la matriz de acceso.
Hacemos i<-1, V(1) = V = {V1, V2, V3, V4, V5}
Tomamos un vértice de V(1) , Por ejemplo V2.
Primera componente conexa: R(V2) ∩ Q(V2)
R(V2) ∩ Q(V2) = {V2, V4} ∩ {V1, V2, V3, V4, V5} = {V2, V4}
V(2) = V(1) ≈ R(V2) ∩ Q(V2) = {V1, V3, V5} es decir, restamos a V(i) lo que obtenemos de realizar la intersección entre R(V2) y Q(V2).
Tomamos lo que obtenemos que hemos denominado V(2) y elegimos un vértice de dicho conjunto, una vez hecho repetimos el procedimiento que expliqué al principio.
Tomamos un vértice de V(2) , por ejemplo, V1.
Segunda componente conexa: R(V1) ∩ Q(V1).
R(V1) ∩ Q(v1) = {V1, V2, V3, V4, V5} ∩ {V1, V3, V5} = {V1, V3, V5}
V(3) = V(2) ≈ R(V1) ∩ Q(V1) = ø
Hemos obtenido el conjunto vacío, lo que nos indica que hemos terminado, por lo tanto las componentes conexas son las V(i) que hemos obtenido:
{V2, V4}, {V1, V3, V5}
Gráficamente quedaría de la siguiente forma:
Método 2 – Multiplicación de matrices
Este método es fácil de realizar si sabemos multiplicar matrices.
El procedimiento es el siguiente:
-Hayamos la matriz de accesibilidad y la matriz de acceso.
-Multiplicamos ambas matrices término a término, es decir, R1,1 x Q1,1; R1,2 x Q1,2; etc…Esto nos dará la matriz RxQ.
Dentro de la matriz tendremos tantas filas como vértices y tendremos que ir fila a fila y columna a columna viendo si aparece un uno o un cero, si aparece un uno entonces ese vértice de la columna forma parte de una componente conexa. Es posible que aparezcan filas repetidas, esto se debe a que no tenemos por qué tener el mismo número de componentes conexas que de vértices, las filas que se repiten hacen alusión a la misma componente conexa.
RECORRIDO DE ARISTAS
Es interesante averiguar si es posible recorrer un grafo pasando por cada arista una sola vez ya que en grafos complejos no es tan fácil de ver.
Para introducir los siguientes conceptos voy a contar una historia que puso las bases de los grafos.
“Problema de los puentes de Königsberg”: Königsberg era una ciudad que estaba separada en 4 partes y conectadas dichas partes unas con otras por 7 puentes. Pero surgió una pregunta, ¿es posible salir de un punto de la ciudad y, pasando por todos los puentes una única vez, volver al mismo punto?.
Leonhard Euler lo resolvió introduciendo el concepto de grafo euleriano.
Sea G un grafo conexo y en general no simple:
1 – Llamaremos tour de G a una cadena cerrada que atraviesa cada arista de G al menos una vez.
2 – Llamaremos tour euleriano de G a un tour de G que atraviesa cada arista exactamente una vez.
3 – Llamaremos grafo euleriano a aquel en el que podemos encontrar un tour euleriano.
4 – Llamaremos camino euleriano a una cadena (simple) que atraviesa cada arista exactamente una vez.
Para ver si un grafo tiene un tour euleriano (y por lo tanto es un grafo euleriano) o si tiene un camino euleriano tenemos varios argumentos con los que descartar el tour euleriano, el camino euleriano o ambos:
-Para que el grafo pueda tener un tour euleriano, no debe tener vértices de grado impar.
-Para que el grafo pueda tener un camino euleriano, debe tener exactamente dos vértices de grado impar.
La forma de calcular un tour euleriano y un camino euleriano viene dado por el algoritmo de Fleury.
ALGORITMO DE FLEURY
Grafo no dirigido
Para calcular un tour euleriano en un grafo no dirigido partimos de vi y terminamos en vi. Vamos a ir construyendo una cadena simple de forma que no se repitan aristas y que no se elijan aristas de corte a no ser que no haya otra alternativa, estas aristas de corte son aquellas que al quitarlas, dejan vértices aislados. Cada arista que vamos eligiendo y eliminando la añadimos al tour euleriano. Terminaremos cuando hayamos llegado desde vi a vj y no queden aristas.
Para calcular un camino euleriano partimos de un vértice vi de grado impar y llegamos al otro vértice de grado impar. El proceso que seguimos de un vértice al otro es el mismo que para el tour euleriano.
Modificación para grafos dirigidos
El proceso es el mismo, para calcular el tour euleriano debemos tener cuidado y al eliminar arcos no debemos elegir un arco que al eliminarlo aumente el número de componentes conexas del grafo no dirigido asociado, a no ser que no tengamos otra alternativa.
Para calcular el camino euleriano debemos empezar por un vértice de grado impar y terminar en el otro vértice de grado impar, de la misma forma que hacíamos en el grafo no dirigido, para ver si un vértice de un grado dirigido tiene grado impar se puede hacer comprobar que:
de(p) = ds(p)-1, de(q) = ds(q)+1
Siendo p y q los vértices inicial y final respectivamente del camino.
EJEMPLO
Teniendo el siguiente grafo no dirigido:
Como podemos ver no hay vértices de grado impar, luego puede haber un tour euleriano y no va a haber un camino euleriano.
Empezamos por el V4 por ejemplo, ya que tenemos menos riesgo de quitar una arista de corte, como estamos buscando un tour euleriano sabemos que debemos volver a este vértice al final del tour euleriano.
Quitamos la arista e3 y llegamos al vértice V3, como todo ha sido correcto pues no queda ningún vértice aislado podemos añadir la arista e3 al tour euleriano y seguir con el proceso.
Esto iremos haciéndolo vértice a vértice y arista a arista hasta llegar nuevamente a V4.
Si alguien tiene alguna duda le paso el ejercicio completo, con imágenes de todo el proceso, de todas formas el tour resultante por si alguien lo intenta y quiere ver si lo hizo bien: e3 e4 e10 e9 e7 e1 e5 e8 e6 e2.
CICLO Y CAMINO HAMILTONIANO
Un camino Hamiltoniano en un grafo G es un camino que atraviesa cada vértice del grafo exactamente una vez.
Un ciclo Hamiltoniano en un grafo G es un ciclo que atraviesa cada vértice del grafo exactamente una vez.
Un grafo es Hamiltoniano si existe un ciclo hamiltoniano.
Reglas básicas para construir caminos y ciclos hamiltonianos
Regla 1 – Si G no es conexo, no posee ciclos Hamiltonianos.
Regla 2 – Si G es un grafo con “n” vértices, entonces un camino Hamiltoniano debe tener exactamente n-1 aristas, y un ciclo Hamiltoniano n aristas.
Regla 3 – Si v es un vértice del grafo, entonces un camino Hamiltoniano debe tener al menos una arista incidente con v y como mucho dos.
Regla 4 – Si G es Hamiltoniano, entonces dG(v) >=2, donde todos los vértices pertenecen a V.
Regla 5 – Si v perteneciente a V tiene grado 2, entonces las dos aristas incidentes con v deben aparecer en cualquier ciclo
Hamiltoniano de G.
Regla 6 – Si v perteneciente a V tiene grado mayor que 2, entonces cuando se intenta construir un ciclo Hamiltoniano, una vez que se pase por v, las aristas no utilizadas incidentes se dejan de tener en cuenta.
Regla 7 – Al construir un ciclo o camino Hamiltoniano para G, no se puede dar el caso de obtener un ciclo para un subgrafo de G a menos que contenta todos los vértices de G.
No podemos calcular si un grafo es Hamiltoniano en estos momentos, ni si tiene ciclos o caminos Hamiltonianos, lo único que podemos hacer es ver si no se cumple alguna de estas reglas y demostrar que NO lo es.
A raiz de todo lo mencionado tenemos el siguiente teorema:
Sea G un grafo dirigido bipartido con partición {X, Y}.
(1) Si G tiene un ciclo Hamiltoniano, entonces card(X) = card(Y).
(2) Si G tiene un camino Hamiltoniano, entonces card (X) y card(Y) difieren a lo sumo en 1.
El recíproco es cierto para grafos bipartidos completos con más de 2 vértices.
Recordad la lógica de primer orden, que un grafo no sea Hamiltoniano no quiere decir que card(X) != card(Y).