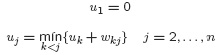Sesión correspondiente al día (21/12/2010).

Grafo ponderado

Definición y ejemplos

1- Un grafo simple G = (V, A) (grafo simple dirigido, respectivamente) diremos que es un grafo ponderado si tiene asociado una función W: A -> R llamada función de ponderación.

La imagen de cada arista (arco, respectivamente) determinada por los vértices v_i y v_j la llamaremos peso de la arista (arco) y lo denotaremos por w_ij.

2- Sea G = (V, A) un grafo ponderado finito tal que V = {v1, …, vn}. Llamaremos matriz de peso del grafo G a la siguiente matriz de orden n x n

3- En un grafo ponderado llamamos peso de un camino a la suma de los pesos de las aristas (arcos respectivamente) que lo forman.

4- En un grafo ponderado llamamos camino más corto entre dos vértices dados al camino de peso mínimo entre dichos vértices.

5- En un grafo ponderado llamaremos camino más largo o camino crítico entre dos vértices al camino de peso máximo entre dichos vértices.

Como siempre la teoría está muy bien para quien la entienda, aquí va un ejemplo que espero que os ayude más:

EJEMPLO

Caminos  más cortos

Supondremos  que los pesos asociados a los arcos son todos no negativos y que el grafo es dirigido. Supondremos además que los vértices del grafo están numeradores de 1 a n, de forma que w_ij representa el peso del arco (i, j) y que el vértice 1 es el origen del camino. Además u_j denotará el peso del camino más corto de 1 a j.

Dicho de otra forma, vamos a suponer que el peso es siempre positivo y que el grafo es dirigido, además numeraremos los vértices del grafo de 1 a n.

Además debemos saber que cada sección a su vez es el camino más corto que se puede considerar. Esto viene demostrado por el siguiente teorema.

Teorema

Sea 1, …., k, …..,j un camino más corto entre los vértices 1 y j de un grafo ponderado G. Entonces las secciones de este camino 1, …., k y k, …., j son los caminos más cortos entre los vértices respectivos.

Tenemos pues que si tenemos un camino de 1 a 3 pasando por 2, podemos considerar que el camino de 1 a 2 y el camino de 2 a 3 son los caminos más cortos también de las respectivas secciones.

Corolario

Supongamos que en un grafo ponderado tenemos un camino más corto entre los vértices 1 y j. Sea k el vértice inmediatamente anterior a j en ese camino. Entonces la sección de este camino desde 1 a k es el camino más corto entre estos dos vértices. Además se cumple que:

u_j = u_k + w_kj

Con esto y las ecuaciones de Bellman podemos calcular el camino más corto:

Ecuaciones de Bellman

Grafos acíclicos. Método del camino crítico o camino más largo

Un grafo dirigido no tiene circuitos si y sólo si existe una numeración de los vértices para la que se cumple que si (i, j) es un arco del grafo entonces i < j.
Con esta numeración, las ecuaciones de Bellman pueden ser reemplazadas por:

Algoritmo de numeración

Antes de lanzarnos a realizar un problema debemos aprender a numerar los vértices ya que como puse más arriba, es una condición necesaria. Para ordenarlos podemos seguir el siguiente algoritmo de ordenación:

Etapa 1. Inicializar i<-i, V⁽¹⁾= V

Etapa 2. Tomar v E V⁽ⁱ⁾ tal que de(v)=0 en G[Vi].

Etapa 3. Numerar el vértice V como vértice 2

-Hacer V⁽ⁱ⁺¹⁾ = V⁽¹⁾ – {V}

-Hacer i<-i+1

Etapa 4. Si V⁽ⁱ⁾ = ø

Algoritmo de Pert

También es interesante comentar la utilizadad del algoritmo de Pert:

Se denomina camino más largo entre dos vértices dados, al camino de peso máximo entre dichos vértices. Un ejemplo típico de obtención de un camino más largo en un grafo dirigido, es la secuenciación de actividades, también llamada red de actividades.
Así por ejemplo, un proyecto de construcción grande se suele dividir en varias actividades menores; estas actividades están relacionadas, en el sentido de que algunas no pueden comenzar hasta que otras hayan finalizado. Por ejemplo, para la construcción de una casa son necesarios cimientos, muros, carpintería, tejados, instalación eléctrica, … Una actividad como la instalación eléctrica, no puede empezar hasta haber completado otras actividades. La realización de este tipo de proyectos hace necesaria una planificación racional de las actividades a realizar que se denomina PERT (Program Evaluation and Review Technique). Para planificar un proyecto de esta clase podemos representar cada actividad de las que se compone el proyecto por un vértice. En este caso el peso lo tomamos como el tiempo necesario para realizar una actividad, por ello vamos a hacer las actividades que más tiempo requieran y así que puedan hacerse también las que requieran menor tiempo, si lo hacemos al contrario las actividades que requieran más tiempo no podrían realizarse por completo.