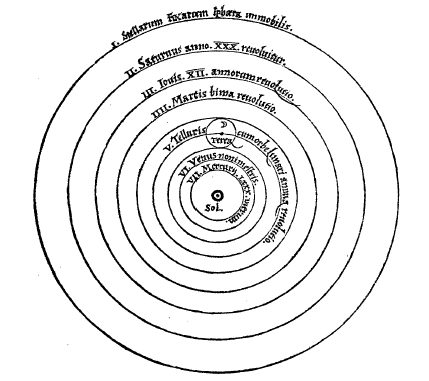
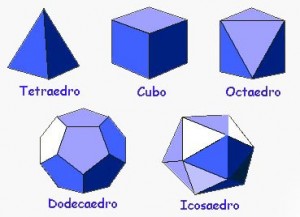
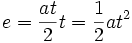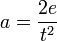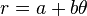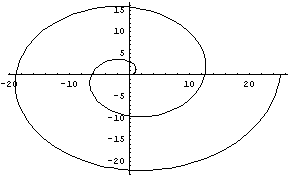Los últimos años de Galileo

Posted on 15 junio, 2011 by sukicorleone

Condenado como vimos en el anterior post a la reclusión domiciliaria, se traslado a su villa en Arcetri, ya aquejado de ceguera (se cree que por la constante visión hacia el sol) y de artritis, aun tuvo fuerzas de completar la última y más importante de sus obras: los “Discorsi e dimostrazioni matematiche intorno à due nueve scienze“, publicado en Leiden por Luis Elzevir en 1638. En ella, partiendo de la discusión sobre la estructura y la resistencia de los materiales, Galileo sentó las bases físicas y matemáticas para un análisis del movimiento, que le permitió demostrar las leyes de caída de los graves en el vacío y elaborar una teoría completa del disparo de proyectiles. La obra estaba destinada a convertirse en la piedra angular de la ciencia de la mecánica construida por los científicos de la siguiente generación, con Newton a la cabeza.

Discorsi e dimostrazioni matematiche intorno à due nueve scienze

Los últimos años los paso rodeado de sus dos discipulos Viviani y Torricelli, con los que pudo debatir sobre ciencia hasta su muerte en 8 de enero de 1642, asi termina una de las vidas más interesantes y activas de este periodo, a la altura de otro gran genio como Erasmo de Roterdam.

La tumba de Galileo Galilei, se puede visitar en la Santa Croce de Florencia, pudiendo darle un último adios, cualquier vistante que pase por esta mágica ciudad.

Tumba de Galileo

Posted in Vida y Obras | Comments Off on Los últimos años de Galileo

Galileo Galilei: La Iglesia contra él.

Posted on 14 junio, 2011 by sukicorleone

Todo comienza con la publicación de su obra clave Sidereus nuncius (conocido como Mensajero sideral, y también bajo la acepción de Mensaje sideral) es un tratado corto escrito en Latín por Galileo Galilei y publicado en Venecia en marzo de 1610. Fue el primer tratado científico basado en observaciones astronómicas realizadas con un telescopio. Contiene los resultados de las observaciones iniciales de la Luna, las estrellas y las lunas de Júpiter. Su publicación se considera el origen de la moderna astronomía y provocó el colapso de la teoría geocéntrica.

En sus observaciones de la Luna Galileo observó que la línea que separa el día de la noche (terminador) poseía irregularidades en las áreas brillantes siendo mucho más suave en las zonas oscuras. De estas observaciones dedujo que las regiones oscuras son planas y de poca altitud, mientras que las regiones brillantes estarían cubiertas por irregularidades orográficas. A partir de la distancia de las montañas iluminadas cerca del terminador estimó que su altura era cercana a los 6 km contradiciendo la establecida cosmología aristotélica que afirmaba que los cielos son perfectos y los cuerpos celestes esferas perfectas.

Observando las estrellas Galileo descubrió más de diez veces más estrellas con su telescopio que con el ojo desnudo publicando cartas celestes del cinturón de Orión y de las Pléyades. Cuando observó las estrellas nebulosas descritas en el Almagesto de Ptolomeo descubrió que en vez de ser regiones nebulares estaban formadas de multitud de estrellas indistinguibles al ojo humano. De este hecho dedujo que las nebulosas y la propia Vía Láctea estaban formadas por conjuntos de estrellas demasiado pequeñas y cercanas para ser identificadas individualmente por el ojo desnudo.

Es sin embargo en la última parte del Sidereus nuncius en la que Galileo muestra sus descubrimientos más importantes. Galileo informa de sus observaciones de cuatro estrellas cercanas a Júpiter y de su movimiento alrededor del planeta. En el Sidereus presenta observaciones de sus posiciones relativas entre enero y marzo de 1610. Del hecho de que estos astros cambiaban su posición relativa noche tras noche conservando siempre la orientación en una misma línea recta dedujo que se trataba de lunas de Júpiter.

Sidereus Nuncius

Aesta obra polémica, pero totalmente cientifica y con datos ciertos, se le une la marcha de Galileo Galilei de Padova a Firenze (Florencia), en 1610, al aceptar el puesto de Primer Matemático de la Universidad de Pisa (sin carga de cursos, ni obligación de residencia) y aquél de Primer Matemático y Primer Filósofo del gran duque de Toscana; esto sera clave, pues pierde la protección de la República de Venecia frente a la Santa Sede.

Asi tras pequeñas disputas menores, con algun eclesiastico, el cardenal Belarmino, inquisidor de gran prestigio, comienza a investigar a Galileo en 1611.
Tras varios años donde Galileo Galilei intento convencer a todos de que sus teorias eran ciertas, en 1616 se dictamino que la teoría heliocéntrica era herética y el cardenal Belarmino, , le advirtió de que no debía discutir ni escribir sobre ella. Galileo obedeció esta consigna durante varios años. Pero la llegada al solio pontifical de Urbano VIII, un hombre culto con el que Galileo tenía relación desde hacía tiempo, le hizo concebir la esperanza de que podría publicar una obra sobre la cuestión.

En 1622, el cardenal Mafeo Barberini (amigo de Galileo Galilei) es elegido Papa bajo el nombre de Urbano VIII. El 3 de febrero de 1623 Galileo recibe la autorización para publicar su Saggiatore que dedica al nuevo Papa. Il Saggiatore, obra donde ridiculizaba a Horazio Grassi, uno de los más importantes científicos jesuitas, que se había eregido como defensor de la teoría geocéntrica contra las ideas de Galileo Galilei.

Esta obra además sirvió para que Galileo expusiera su método científico resolutivo – compositivo, y para reafirmar todos sus descubrimientos e hipotesis.

Il saggiatore

Con Urbano VIII, Galileo podrá trabajar sin problemas con la inquisición hasta el año 1632, año en el que publica “Diálogo sobre los principales sistemas del mundo” donde se burla implícitamente del geocentrismo de Ptolomeo. El Diálogo es a la vez una revolución y un verdadero escándalo. El libro es en efecto abiertamente pro-copernicano.

El Diálogo se desarrolla en Venecia durante cuatro jornadas entre tres interlocutores: Filipo Salviati, un Florentino seguidor de Copérnico, Giovan Francesco Sagredo, un veneciano ilustrado sin tomar partido, y Simplicio, un mediocre defensor de la física aristotélica, un personaje que algunos quieren ver inspirado en Urbano VIII.

Pese a que Galileo Galilei, declara que no se basaba en urbano VIII, pierde el favor del Papa y su unica defensa contra la Inquisición, que aprovechara para condenarle definitivamente en el año 1633, juicio donde a Galileo, se le condena a prisión perpetua, y se le conmina a abjurar de sus ideas, cosa que hace seguidamente. Tras la abjuración el Papa conmuta la prisión por arresto domiciliario de por vida.
Se cree que en este momento es cuando Galileo dijo su famosa frase “Eppur si muove” (y sin embargo se mueve) reafirmándose en sus ideas heliocéntricas.

 

Posted in iglesia vs ciencia | Comments Off on Galileo Galilei: La Iglesia contra él.

Galileo Galieli y la astronomía

Posted on 14 junio, 2011 by sukicorleone

Si tenemos que destacar algun campo de la ciencia, donde Galileo Galilei brillara de especial manera, este no sería otro que la Astronomía. Así que hoy hablaremos de las aportaciones de Galileo en este campo.

Ya nombramos con anterioridad, que Galileo Galilei perfecciono el telescopio, sin duda parte fundamental de todos sus descubrimientos en este campo, y que le llevo a confirmar la teoría heliocéntrica expuesta por Copérnico.

– En primer lugar, aplicando su metodo de estudio, rechazo las ideas de Artistoteles (pese a que en la época, era el cientifico con mayor repercusión en la sociedad) en su teoria de mundo sublunar (la Tierra y todo lo comprendido entre el planeta y la Luna; un mundo imperfecto y cambiante) y traslunar (la Luna y más allá; un espacio con formas geométricas perfectas y movimientos regulares)

– Además gracias al telescopio, pudo observar las montañas y valles de la luna, por lo que pudo demostrar que la superficie lunar no era llana, tal como afirmaban los aristotélicos.

– Pudo observar los 4 satelites de Jupiter los llamados “astros mediceos” y comprobar que giraban en torno a Jupiter, y no alrededor de la tierra como se creía y se formulaba en la epoca, que todos los astros giraban alrededor de la tierra.

Los 4 satélites de Júpiter

– En la linea de confirmar su teoría de que el mundo traslunar si que era cambiante, confirmo la existencia de las manchas solares, el sol estaba en continuo cambio, contrario a las ideas aristotélicas.

– Pudo observar la Via Lactea y afirmar que era un conjunto de estrellas.

– Descubrió el anillo de Saturno, pero la aun baja calidad del telescopio, le llevo a creer que eran satélites.

– Descubrió las fases de Venus y de Marte, solo aceptadas si se daba como ciertas las teorías de Copérnico.

La mayoría de estsos descubrimientos, los hizo Galileo Galilei en el observatorio astronómico de Padova, “La Specola” lugar que aun se conserva en padova, y que con solo observarla desde fuera se puede notar el aire a ciencia que respira todo lo procedente a Galileo Galilei.

La specola, observatorio astronómico de Padova, actualmente sede del departamento de Astronomía de la universaidad de Padova

Las observaciones que, con el telescopio, realizó Galileo aportaron las pruebas más fuertes en favor del heliocentrismo, que pueden ser enumeradas del siguiente modo:

– Las fases de Venus, unidas a su variación de tamaño, son sólo compatibles con el hecho de que, gire alrededor del Sol, ya que presenta su menor tamaño cuando se encuentra en fase llena y el mayor, cuando se encuentra en la nueva; es decir, cuando está entre el Sol y la Tierra, El hecho de que, sin la ayuda del telescopio, no se apreciaran las necesarias variaciones de luminosidad de Venus, si se quería que éste girase en torno al Sol, se explicaba entonces claramente también por la disminución de la superficie iluminada visible desde la Tierra cuando el planeta está más próximo a ella. Además, por sus fases, Venus resultaba ser, lo mismo que la Luna, un cuerpo obscuro.

– El descubrimiento de las montañas de la Luna, la hacían similar a la Tierra.

– Los satélites de Júpiter suponían que la Tierra no sería el único caso de cuerpo girando alrededor del Sol, sobre el que, a su vez, gira otro. Estos tres puntos implicaban que, al margen de las estrellas y cometas, todos los cuerpos del Universo, excepto el propio Sol, eran semejantes entre sí.

– El menor tamaño angular de las estrellas evitaba los inconvenientes de Tycho al modelo de Copérnico en el sentido dé que si la esfera de las estrellas fijas se hacía suficientemente grande para que no fueran apreciables efectos de paralaje por el movimiento orbital terrestre, las estrellas deberían ser enormes.

Vemos, en definitiva que las pruebas en favor del heliocentrismo aportadas por Galileo son de carácter fundamentalmente empírico y en absoluto basadas en elucubraciones simplemente mentales. Es cierto que Galileo, como Copérnico,. Tycho o Kepler, es un platónico. Pero en el sentido, de que para él, lo mismo que para los otros tres, el Universo ha de poder ser explicado mediante los números, pero Galileo no elucubra sobre si la naturaleza cristalina o no de la Luna existen las montañas porque él (o cualquier otro, con ayuda del un telescopio) puede observarlas. No elucubra sobre si Venus debe moverse o no alrededor de la Tierra. Sencillamente, verifica con sus propios ojos, que gira alrededor del Sol.

Todo esto le llevo a continuas discusiones con los teóricos eclesiásticos, hasta su persecución por la inquisición, tema que abordaremos en el siguiente post.


Posted in ciencia, Descubrimientos, Investigaciones, Padova | Comments Off on Galileo Galieli y la astronomía

Galileo Galilei: El método científico resolutivo-compositivo

Posted on 14 junio, 2011 by sukicorleone

Galileo Galilei, es uno de los cientificos más importantes de la edad moderna, por su grandes aportes a la ciencia, especialmente en el metodo de trabajo, que usaba para llegar a sus conclusiones y formular sus hipotesis, este metodo es el llamado “método científico resolutivo-compositivo”

El método se basaba en 4 pautas a seguir:

1.- Observación:
Hay que partir inevitablemente de la precisión en la consideración del objeto de la investigación, lo que únicamente es posible por la determinación de datos de observación minuciosamente delimitados y con referencia a un problema que resolver. Generalmente el problema que se plantea hace referencia a una teoría explicativa frente a la cual los datos observados no pueden ser explicados por ella, bien por un cambio de concepto en el fundamento o por simple ampliación de observaciones.

2.- Elaboración de una hipótesis explicativa:
A partir de este momento la explicación de este nuevo modo de concebir el fenómeno requiere una explicación nueva, lo cual se hace como hipótesis o teoría provisional a la espera de una confirmación experimental.

3.- Deducción:
Sobre esta hipótesis o teoría se hace necesario extraer las consecuencias que se derivan del hecho de tenerla por verdadera. Fundamentalmente dichas consecuencias deductivas deben ser de tipo matemático pues, como dice Galileo, la naturaleza está escrita en lenguaje matemático

4.- Experimento o verificación
Se montan las condiciones en las que se puedan medir las consecuencias deducidas, procurando unas condiciones ideales para que las interferencias con otros factores sean mínimos (rozamientos, vientos etc.), y comprobar si efectivamente en todos los casos, siempre se reproducen dichas consecuencias.

Por ejemplo en la formulación de la ley de movimiento de los cuerpos

1.- Galileo rechaza la teoría aristotélica del movimiento. No acepta la explicación cualitativa. Él pretende una descripción del movimiento por la medida de cantidades, como relación espacio-tiempo que permite establecer lo que él llamó cantidad de movimiento que hoy llamamosvelocidad. La caída libre de los graves, percibida en la experiencia como ir cada vez más deprisa se convierte ahora en una relación meramente cuantitativa de variación de cantidad de movimiento por unidad de tiempo, lo que hoy llamamos aceleración.
Ahora el movimiento de caída de los graves se interpreta como variación de relación de cantidades: en un primer orden de espacio y en un segundo orden de velocidad, con respecto al tiempo.
2.- Galileo considera tres tipos de hipótesis: las metafísicas que no tienen comprobación alguna, las inventadas para salvar la situación, como explicación de las apariencias, y las deductivas pensadas para poder obtener de ellas nuevas relaciones matemáticas entre los elementos de la observación. Estas son las que realmente interesan a la ciencia.
Galileo establece la hipótesis que le parece razonable: la variación de la cantidad de movimiento (velocidad) en el movimiento de caída libre es constante. Dicho modernamente: la aceleración es constante.
3.- Galileo en su caso realizó las siguientes deducciones:
Naturalmente simplificamos y utilizamos conceptos y expresiones matemáticas actuales
Sobre la hipótesis de que en el movimiento de caída de los cuerpos la aceleración es constante, tendríamos las siguientes relaciones:
Velocidad final del móvil: Vf = V0 + at
Velocidad media del móvil: V_m={V_0+V_f\over 2}
Espacio recorrido por el móvil: e = Vmt

 

En el caso de que el móvil iniciara el movimiento desde el estado de reposo, entonces:
V0 = 0 y entonces:
Vf = at;
V_m={V_f\over 2}={at\over2};
y el espacio recorrido: e={at\over2}t={1\over2}at^2
y finalmente: a={2e\over t^2}

 

Con estas deducciones tenemos un medio de comprobación de la hipótesis pues hemos deducido el valor de la aceleración en función de los valores del espacio recorrido, que es medible, y el tiempo, que también es medible. (Lo que no ocurre con la velocidad o la aceleración con los medios disponibles en la época). Lo que nos permitiría construir una experiencia, ahora experimento, para comprobar que el valor de dicha aceleración es siempre la misma, constante.
4.- No es cierto que Galileo se dedicase a lanzar cuerpos desde la torre inclinada de Pisa. En su lugar construyó unas rampas bien preparadas y unas bolas de bronce bien pulidas para minimizar los rozamientos. Tras numerosas mediciones halló un valor medio que vino a ser, con sus instrumentos de medida, 9,6 m/s2.

Este metodo, fue usado por muchos filósofos, para aplicarlos a las formulaciones políticas de la época, caso de Hobbes, Grocio o Spinoza

Posted in ciencia | Comments Off on Galileo Galilei: El método científico resolutivo-compositivo

Galileo Galilei en Pádova (1592-1610)

Posted on 8 junio, 2011 by sukicorleone

Galileo Galilei, se marcha de Pisa, por supuestas malas relaciones con por diferencias con uno de los hijos del gran duque Fernando I de Toscana, hacia la Universidad de Padova, que como ya nombramos en anteriores post, pertenecía a la República de Venecia, con la consiguiente cierta independencia que tenía frente a la iglesia.

Galileo dio clases de Mecánica Aplicada, Matemática, Astronomía y Arquitectura militar; desde el año 1592 hasta el año 1610, años que pese a problemas económicos (por la muerte de su padre en 1591, lo que hizo que tuviera que mantener a su familia) fueron de gran felicidad para Galileo, por ser los años donde desarrollo sus teorias, y puso en marcha su gran invento, el telescopio (inventado por Hans Lippershey, pese a que existen varias discusiones acerca de su autoria, fue Galileo quien lo perfecciono, y exploto su uso) llegando a ver con él 4 lunas de Jupiter, o los valles lunares.

En el año 1604, Galileo demuestra teóricamente que los cuerpos que caen, siguen lo que se dio en llamar la ley del movimiento uniformemente acelerado, según la cual, en tal movimiento, los cuerpos aumentan o disminuyen de velocidad uniformemente con el tiempo.

Tambien demostró, el movimiento parabólico de los proyectiles en un espacio vacío, algo que concretaría Isaac newton con la Ley de la Gravedad, demostrando que en verdad siguen trayectorias elípticas.

Inventa el termoscopio, antecesor del termometro. El termoscopio estaba compuesto por una bola de vidrio hueca y un tubo soldados a esta.

Funcionaba de la siguiente forma: Se calentaba la bola de vidrio con las manos y el extremo del tubo se sumergía en agua contenida en una especie de vaso. Una vez enfriada la bola al retirarle las manos. El agua ascendía y marcaba la temperatura. Sirve para comparar diferencias de temperatura, es decir, no mide porque no tiene escala, solo compara la temperatura entre dos cuerpos.

Esquema de un termoscopio

En 1609, tras oir el rumor de la invención de un telescopio construido en Holanda, que permite ver la estrellas que a simple vista es imposible ver, Galileo sin ver ningun plano del original, construye su primer telescopio. Al contrario que el telescopio holandés, éste no deforma los objetos y los aumenta 6 veces, o sea el doble que su oponente. También es el único de la época que consigue obtener una imagen derecha gracias a la utilización de una lente divergente en el ocular. Este invento marca un giro en la vida de Galileo.

El 21 de agosto, apenas terminado su segundo telescopio (aumenta ocho o nueve veces), lo presenta al Senado de Venecia. La demostración tiene lugar en la cima del Campanile de la plaza de San Marco. Los espectadores quedan entusiasmados: ante sus ojos, Murano, situado a 2 km y medio, parece estar a 300 m solamente. (en la actualidad existe una placa en la torre campanille que recuerda este hecho)

Galileo ofrece su instrumento y lega los derechos a la República de Venecia, muy interesada por las aplicaciones militares del objeto. En recompensa, es confirmado de por vida en su puesto dePadua y sus emolumentos se duplican.

Este invento, hizo que Galileo Galilei, se centrara en la astronomía, y revolucionara esta ciencia, confirmando las teorias de Copernico, pero este tema lo abordaremos en el siguiente post, donde veremos toda la información referente a Galileo y la astronomía.

Como curiosidad, referir que actualmente en la Universidad de Pádova se conserva la cátedra de Galileo Galilei (especie de púlpito donde daba clase), así como su busto, y un retrato de él, presente en el aula magna de dicha Universidad, que puede verse todos los días en horario de visita, y por solo 3 euros adultos, y gente universitaria de forma gratuita.

Catedra y busto de Galileo Galilei

Retrato de Galileo presente en el aula Magna de la Universidad de Padova

Posted in ciencia, Descubrimientos, Padova, Vida y Obras | Comments Off on Galileo Galilei en Pádova (1592-1610)

La gran influencia de Galileo: Nicolás Copérnico

Posted on 6 junio, 2011 by sukicorleone

Si alguien revoluciono la forma de ver la astronomía antes de Galileo Galilei, este fue Nicolás Copérnico, el primer cientifico que escribio sobre la teoría heliocentrista (ya los autores clásicos griegos habían dado datos sobre esta teoría, pero Copérnico, fue el primero en un periodo regido por las teorias eclesiásticas, donde la tierra era el centro del universo) asi que no nos parece justo, hablar de los descubrimientos de Galileo Galilei en Padova, sin antes hacer un pequeño resumen de la vida de este científico.

Nicolás Copérnico (Toruń, Prusia, Polonia, 19 de febrero de 1473 – Frombork, Prusia,Polonia, 24 de mayo de 1543)

Nicolás Copérnico

Este famoso científico polaco-prusiano2 estudió en la Universidad de Cracovia (1491-1494) bajo las directrices del matemático Wojciech Brudzewski. Viajó por Italia y se inscribió en la Universidad de Bolonia (1496-1499), donde estudió Derecho, Medicina, Griego, Filosofía, y trabajó como asistente del astrónomo Domenico da Novara.

En 1500 fue a Roma, donde tomó un curso de ciencias y astronomía, y en 1501 volvió a su patria y fue nombrado canónigo en la Catedral de Frauenburg, cargo obtenido merced a la ayuda de su tío Lucas Watzenrode.

Pese a su cargo, volvió a Italia, esta vez a Padua (1501-06), para estudiar Derecho y Medicina, haciendo una breve estancia en Ferrara (1503), donde obtuvo el grado de Doctor en Derecho Canónico.

Reinstalado definitivamente en su país (1523), se dedicó a la administración de la diócesis de Warmia, ejerció la Medicina, ocupó ciertos cargos administrativos y llevó a cabo su inmenso y primordial trabajo en el campo de la Astronomía. Falleció el 24 de mayo de 1543 en Frombork, Polonia.

Hacia 1507, Copérnico elaboró su primera exposición de un sistema astronómico heliocéntrico en el cual la Tierra orbitaba en torno al Sol, en oposición con el tradicional sistema tolemaico, en el que los movimientos de todos los cuerpos celestes tenían como centro nuestro planeta. Una serie limitada de copias manuscritas del esquema circuló entre los estudiosos de la astronomía, y a raíz de ello Copérnico empezó a ser considerado como un astrónomo notable; con todo, sus investigaciones se basaron principalmente en el estudio de los textos y de los datos establecidos por sus predecesores, ya que apenas superan el medio centenar las observaciones de que se tiene constancia que realizó a lo largo de su vida.

Todas estas ideas, las plasmo en su obra clave “De revolutionibus orbium coelestium”

Obra De revolutionibus orbium coelestium

Fue escrita a lo largo de unos veinticinco años de trabajo (1507-32) y fue publicada póstumamente el 1543.
Copérnico estudió los escritos de los filósofos griegos buscando referencias al  del movimiento terrestre, especialmente los pitagóricos y heráclides póntico quienes creían en dicha . en cuanto a la teoría heliocéntrica en sí, hasta donde se sabe hoy, fue concebida por  vez poraristarco de samos (310-230 a. c.), a quien curiosamente no nombra en su obra.[2] es preciso centrar el valor real de sus estudios en el hecho de reimponer teorías ya rechazadas por el «sentido común» y de darles una estructuración coherente y científica.

la ruptura básica que representaba para la ideología religiosa medieval, la sustitución de un cosmos cerrado y jerarquizado, con el hombre como centro, por un universo homogéneo e , situado alrededor del sol, hizo dudar a copérnico de publicar su obra, siendo consciente de que aquello le podía acarrear  con la iglesia; desafortunadamente, a causa de una enfermedad que le produjo la muerte, no alcanzó a verla publicada. copérnico aún estaba trabajando en el de revolutionibus orbium coelestium (aunque aún no convencido de querer publicarlo) cuando en 1539 georg joachim rheticus, un matemático de wittenberg, llegó a frombork. philipp melanchthon había arreglado para rheticus su visita a diversos astrónomos y el  con ellos. rheticus se convirtió en el pupilo de copérnico, viviendo con él por dos años, tiempo durante el cual escribió un libro, narratio prima (primer recuento), resumiendo la de la teoría de copérnico. en 1542 rheticus publicó un tratado de trigonometría escrito por copérnico (incluido después en el segundo libro de de revolutionibus). bajo gran presión por parte de rheticus, y habiendo visto la reacción favorable del público frente a su trabajo, copérnico finalmente accedió entregar el libro a su amigo cercano tiedemann giese, obispo of chełmno (kulm), a ser entregado a rheticus para ser impreso por johannes petreius en nuremberg (nürnberg). la primera edición del “de revolutionbus” aparece en 1543 (el mismo año de la muerte del autor), con una larga introducción en la que dedica la obra al papa pablo iii, atribuyendo su motivo ostensible para escribirla a la incapacidad de los astrónomos previos para alcanzar un acuerdo en una teoría adecuada de los planetas y haciendo notar que si su sistema incrementaba la exactitud de las predicciones astronómicas, esto permitiría que la iglesia desarrollara un calendario más exacto (un tema por entonces de gran interés y una de las razones para financiar la astronomía por parte de la iglesia).

el trabajo en sí estaba dividido en seis libros:
1. visión general de la teoría heliocéntrica, y una explicación corta de su concepción del mundo.
2. básicamente teórico, presenta los principios de la astronomía esférica y una lista de las estrellas (como base para los argumentos desarrollados en libros siguientes).
3. dedicado principalmente a los movimientos aparentes del sol y a fenómenos relacionados.
4. descripción de la luna y sus movimientos orbitales.
5. explicación concreta del nuevo sistema.
6. explicación concreta del nuevo sistema (continuado).

Así Copernico de esta manera llegamos a la conclusión de que la idea principal de copérnico fue la de conservar las ideas y principios de la antigüedad pero con otra hipótesis: la del movimiento de la tierra. ptolomeo sólo ofrece una caja de herramientas para resolver problemas, mientras que copérnico unirá todos esos problemas para dar una configuración completa del sistema planetario: un universo finito y cerrado pero con las estrellas infinitamente alejadas, idea que daría píe a que sus sucesores planteasen la idea de un universo infinito. por eso insistimos en que la importancia fundamental de copérnico no fueron sus ideas en sí, sino lo que estas significaron para abrir pico paso a los descubrimientos astronómicos posteriores.

Sistema heliocéntrico de Copérnico

Sistema Heliocentrico, incluido en su obra "De Revolutionibus Orbium Coelestium"

Nicolas Copernico, murio antes de ver publicada su obra, se cree que la tuvo terminada años antes, pero que por miedo a la condena de la Iglesia, espero a publicarla, para evitar que la gente pensara que no era un hombre de fe, dedico esta importantísima obra al Papa Pablo III, pese a ello, esta obra fue motivo de debate y apartado en muchos círculos intelectuales, por su ataque al sistema aristotélico, pese a ello, Galileo Galilei tuvo acceso a esta obra, que sin duda fue la base para las ideas de Galileo Galilei e incluso para científicos posteriores como Isaac Newton

Posted in ciencia, iglesia vs ciencia, Investigaciones | Comments Off on La gran influencia de Galileo: Nicolás Copérnico

La república de Venecia

Posted on 4 junio, 2011 by sukicorleone

Galileo Galilei llega a Padova en 1592, la ciudad universitaria por excelencia, de la rica y prospera Republica de Venecia.

Padova que entro en la Republica de Venecia en el S. XV, participo de la prosperidad de esta república, especialmente con el desarrollo de su universidad, la 2ª más antigua de Italia, fundada en 1222, y que a diferencia de la universidad de Pisa, tenía una menor influencia por parte de la Iglesia, y por tanto mayor libertad a la hora de impartir conocimientos, algo que se vio especialmente en areas como Medicina, donde pudieron diseccionar cuerpos humanos para conocerlo mejor, dando paso a grandes avances, tales como las trompas de Falopio, o exponer teorías en ese tiempo arriesgadas frente a la iglesia, como las expuestas por Galileo Galilei y su sistema heliocentrista.

Pero pasemos a explicar brevemente la historia de la república de Venecia, para comprender mejor el mundo en que vivía Galileo Galilei.

Italia en el siglo XV. Al inicio del siglo XV el territorio italiano se presentaba muy fragmentado en estados de diversa extensión e importancia. El declive de las ciudades había llevado a un proceso de reforzamiento institucional, concluido con la instauración de las signorie (el equivalente a los señoríos ibéricos), junto con las repúblicas oligárquicas, fundadas con anterioridad. De este modo, se formó un pequeño número de estados regionales, de mayor extensión y más fuertes, que poco a poco ampliaron sus propios dominios entrando en concurrencia entre sí con el fin de lograr la supremacía sobre el conjunto. Entre todos ellos, el ducado de Milán se configuró como una potencia emergente, primero bajo la familia de los Visconti, después bajo la de los Sforza, interesada en expandir sus dominios a expensas de las repúblicas de Venecia y de Florencia. Esta última, después de varios conflictos con el Papado y de sofocar revueltas internas de carácter popular, conoció una fase de auge con la llegada de los Medici en 1434. Por su parte, la república de Venecia, desde siempre en lucha con Génova por la supremacía comercial en los mares, extendió poco a poco sus dominios en tierra firme, eliminando pequeñas señorías locales y entrando, por lo tanto, en conflicto con Milán y con el Papado. Los Estados Pontificios, definitivamente concluido el Gran Cisma de Occidente en 1418, se adentró en una fase de estabilidad interna, no obstante los contrastes con las potencias limítrofes. El reino de Nápoles, gobernado por los Anjou, estuvo en el centro de las luchas dinásticas entre las distintas ramas de los angevinos y, poco después, fue conquistado por los aragoneses, que en 1442 unieron los territorios de Cerdeña, Sicilia y Nápoles a las coronas hispanas de Aragón y Castilla. La paz de Lodi puso fin a la rivalidad entre Milán y Venecia y, bajo la égida del Papa, tuvo lugar un pacto entre los cinco mayores estados italianos (Milán, Venecia, Florencia, Estados Pontificios y reino de las Dos Sicilias) que instauró una política de equilibrio destinada a perdurar hasta final de siglo gracias al cual la península quedó a salvo de las intervenciones extranjeras.

Mapa de Italia en el Siglo XV

Tras estos tratados, y estructuración de las fronteras, Venecia pasaba a ser la mayor potencia económica de todo el mediterraneo, gracias especialmente a su comercio con Oriente y sobretodo con el comercio de especias que soldados y peregrinos habían aprendido en Oriente pasó más tarde a las cocinas de la gente corriente. Los venecianos controlaron este comercio hasta el siglo XVI. A principios del siglo XV el comercio de especias movía anualmente 540.000 ducados. En un principio las mercancías de Oriente llegaban a Venecia en barcos bizantinos, pero pronto los venecianos armaron buques propios. A principios del siglo XV 3.000 buques mercantes navegaban bajo bandera veneciana, en su mayoría dedicados al comercio costero y la pesca. El comercio de ultramar estaba cubierto por cerca de 300 barcos que viajaban por su cuenta o en convoyes fuertemente armados que organizaba el estado, la mude. Las aventuras comerciales municipales eran más seguras y la Serenísima cobraba altos precios por la carga en las galeras y por la protección de los convoyes. Los propietarios privados que viajaban sin protección obtenían grandes beneficios por enfrentarse al riesgo. El riesgo personal en los negocios era menor formando una compañía , la colleganza. Por regla general esto se hacía entre dos mercaderes; uno permanecía en Venecia y ponía tres cuartas partes del capital y el cuarto restante era aportado por el que viajaba. La ruta más corriente que hacían lasmude o convoyes iba de Inglaterra a Tana y Trebisonda, en el mar Negro. El principal país con el que comerciaba Venecia era Egipto. Otros puertos importantes eran Beirut y Bizancio. En todas las grandes ciudades los venecianos tenían establecimientos comerciales donde establecían sus negocios y ejercían una considerable influencia política en muchos países. Aunque el comercio de esclavos había sido prohibido oficialmente desde el siglo IX, era una buena fuente de ingresos. Los esclavos se obtenían principalmente en Tana. La trata de circasianos y georgianos, de fe greco-ortodoxa, que eran revendidos en Egipto y el norte de Africa, no repugnaba a la conciencia por no pertenecer a la Iglesia Católica. El comercio de esclavos paganos no estaba prohibido. A mediados del s.XV Venecia preparaba cuatro grandes flotas anualmente escoltadas por galeras armadas.

 

  1. La ruta del mar Negro que, después de llegar a Constantinopla, se dividía en dos: una se dirigía hacia Crimea, mar de Azov, y remontaba el Don hasta Tara, lugar de llegada de las caravanas mongolas y rusas. La segunda se dirigía a Sinope y Trebisonda.
  2. La ruta de Palestina y Siria por Morea, Creta y Chipre.
  3. La de Egipto adonde llegaban las especias por el mar Rojo.
  4. La más larga del Norte de Europa, con escalas en Sicilia, Malta, Trípoli, Túnez, Argel, Orán, Tánger, Lisboa, Burdeos, La Rochelle, Bourgneuf, Brujas, Amberes, Londres y, al regreso, escalas en puertos españoles, provenzales e italianos.

Mas cuando llega Galileo a Padova, Venecia esta en los años de retroceso económico, debido a las disputas contra los turcos, frente a los que habían sufrido varias derrotas, perdiendo el control de parte del Adriatico, Desde 1470 la expansión del Imperio otomano en los Balcanes empezó a preocupar a los venecianos; en 1499-1503 una costosa guerra contra los turcos (quienes desde 1480habían ya llegado a las costas del Adriático) sólo terminó cuando Venecia cedió territorios mediterráneos al Imperio Otomano. En 1538 los venecianos fueron de nuevo vencidos en combate por la flota otomana en Preveza y ello confirmó el predominio naval de Turquía en el Mediterráneo oriental, coincidiendo con el apogeo del Imperio Otomano. En 1570, Chipre sufrió la invasión turca, y un año después los venecianos abandonaban la isla, al no poder detener la invasión otomana. La alianza de las flotas veneciana, papal y española, aunque venció a los turcos en la batalla de Lepanto de 1571, no logró recuperar estos territorios, en parte porque si bien España veía un potencial aliado mediterráneo en Venecia, no estaba dispuesta a sostener con tropas españolas una nueva expansión colonial veneciana.

Habiendo ya aceptado la supremacía naval turca, Venecia se esforzó en mantener su actividad comercial a lo largo del siglo XVII, observando una cuidadosa neutralidad hacia sus vecinos más poderosos: España, el Imperio Otomano, y Francia. Venecia queda eclipsada económicamente por la riqueza de España y su imperio colonial, así como por la gran expansión comercial ultramarina de Inglaterra y Holanda, basada en las rutas ultramarinas del Océano Atlántico que disminuyen grandemente la influencia comercial de Venecia, reducida a un Mediterráneo menos rico y donde debe rivalizar con otros grandes poderes.

Venecia ira perdiendo su poder, hasta que en 1792, solo cuenta con 200 navios para comerciar, una décima parte de lo que había sido su flota, y se convierte en una ciudad con mas de 100 casinos, con una economía destinada al “turismo” de esa época.
En  1797 termina la Republica Italiana, tras la derrota frente a las tropas de Napoleon.

Pero ¿como funcionaba esta República de Venecia? ¿Cual era su funcionamiento político? Desde el primer momento la organización de la república de Venecia, se esforzó por evitar que un solo hombre reuniera todo el poder. De este modo, la función suprema que asumía el dux quedó enseguida sometida a la vigilancia de varios consejos. El Consejo Mayor o Gran Consejo “(Maggior Consiglio)” elaboraba las leyes, el Senado se encargaba de la política exterior y de los asuntos militares y económicos. Otro organismo, “El consejo de los diez” garantizaba la seguridad del estado y disponía de un cuerpo de policía.

La organización política republicana se fue haciendo más compleja a medida que crecía la influencia económica y política de Venecia en el Mar Mediterráneo y tenía que enfrentarse a otras potencias comerciales. En los primeros años de la república el sistema político de gobierno estaba constituido por una autocracia, con el Dux como dictador casi absoluto. Este título comenzó a utilizarse cuando la ciudad de Venecia estaba sujeta a la soberanía del Imperio Bizantino, haciéndose permanente después de que la ciudad alcanzara su independencia respecto de Constantinopla.

De acuerdo a la tradición veneciana, el primer dogo fue Paolo Lucio Anafesto, elegido para el cargo en el año 697, el Dux era elegido de por vida para el cargo, a través de un complicado sistema de inspiración bizantina. Tradicionalmente desde 697 cada dux había asociado a las funciones de gobierno a un hijo u otro familiar, pero rápidamente tal costumbre fue prohibida por ley; en 1172 se estableció la elección del dux por un conjunto de 40 (después 41) ciudadanos, elegidos al azar; en 1268 se fijó el sistema electoral vigente hasta la extinción de la República en 1797 que consitía en una serie de cuatro elecciones, cada una de ellas era seguida de un sorteo entre los ciudadanos elegidos, de donde se formaba el grupo de 41 patricios que finalmente seleccionaban al dux. Tan complejo sistema buscaba evitar la influencia de las familias más ricas e impedir que alguna de ellas (vigilada de cerca por otras familias de igual poder y riqueza) intentase crear una dinastía.

Desde 1148 los poderes del dux fueron limitados por la Promissione Ducale, un compromiso asumido por el Dux en el momento de su nombramiento. Como resultado de ello el poder fue compartido con el Gran Consejo o Consejo Mayor, compuesto de 480 miembros elegidos de determinadas familias de la nobleza, a fin de que “El Dux no podría hacer nada sin el Consejo Mayor y el Consejo Mayor no podía hacer nada sin él”.

En el siglo XII, las familias aristocráticas del Rialto disminuyeron de manera aún más drástica el poder del Dux con el establecimiento del Consejo menor (1175), compuesto por seis miembros asesores del Dux y la Quarantia (1179) como tribunal supremo.

En 1223 estas instituciones se combinaron en la Signoria, que estaba formada por el Dux, El Consejo Menor y los tres dirigentes de la Quarantia. La Signoria era el órgano central de gobierno, que representaba la continuidad de la república, como se muestra en la expresión: “si è morto il Doge, no la Signoria” (“Aunque el Dux esté muerto, no la Signoria”).

También se crearon dos órganos llamados sapientes que se convertirían posteriormente en seis. La combinación de sapientes y algunos otros grupos fue llamado un collegio, que formaba un poder ejecutivo.

En 1229, se instituyó el Consiglio dei Pregadi comúnmente denominado el Senado, compuesto por 60 miembros elegidos por el Consejo Mayor desde el que se dirigía la política exterior y la elección de embajadores. Estos acontecimientos, dejaron al dogo con un poder personal muy reducido y vio cómo la autoridad era ejercida básicamente por el Consejo Mayor, que constituía un extremadamente limitado parlamento, en el que sólo estaban autorizados a participar los miembros de las grandes familias aristocráticas de la república.

Venecia afirmaba que su gobierno era una ‘República clásica’ porque era la combinación de las tres formas básicas presentes: el poder real en el Dux, la aristocracia en el Senado, y el poder democrático en el Consejo Mayor. No obstante la investidura del dux casi siempre recayó en un miembro de las familias más adineradas de Venecia, pues la posesión de dicho cargo obligaba al titular a financiar numerosísimos gastos (fiestas populares, ceremonias lujosas, fiestas del Carnaval, regalos de dinero a aristócratas arruinados) que sólo un hombre muy rico podía sostener.

El 10 de julio de 1310 se estableció el Consejo de los diez, organización similar a una policía secreta del Estado, que se hizo muy poderoso y se convirtió en el eje central de la política veneciana. Fue introducido de forma provisional, como reacción a la rebelión promovida por Bajamonte Tiepolo contra la clausura del Consejo Mayor. Le fueron asignados poderes de emergencia para luchar contra la revuelta y aunque originalmente se estableció para un periodo de dos meses, su autoridad fue renovada de forma continua, hasta que se convirtió en un órgano de carácter permanente.

Mapa de la República de Venecia por parte de P. Daru. Chez Firmin Didot,en el año 1819

Esta era la Venecia que Galileo Galielei vivio pese a estar ya en los años de decadencia, especialmente por la amenaza turca y porque las rutas comerciales se habían trasladado hacia América, Venecia aun tenía el sufiente poder como para poder mostrar cierta dependencia frente al Vaticano, y por tanto la Iglesia tenía un peso reducido en la Universidad de Padova, algo que Galileo Galilei aprovecharía, para poder desarrollar todos sus conocimientos.

 

Posted in Ciudades de interes, iglesia vs ciencia, Padova | Comments Off on La república de Venecia

Grandes matemáticos que influyeron en Galileo y en el pensamiento de la edad Moderna: Arquímedes y las Matemáticas (2ª Parte)

Posted on 3 junio, 2011 by sukicorleone

En el anterior post, pudimos ver un breve resumen de la vida de Arquimedes de Siracusa, así como sus descubrimientos y anecdotas más importantes y de mayor relevancia. Hoy nos centraremos en sus contribuciones al ámbito de las matemáticas, especialmente en el área de la Geometría.

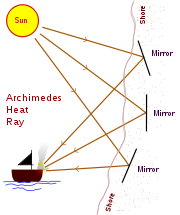
Se conocen hasta 11 obras de Arquimedes, algunas son correspondencia con otros científicos de Alejandría como Eratóstenes o Dositeo; otras obras se conocen por los escritos de Pappus de Alejandría, por ejemplo, menciona Sobre hacer esferas y otro trabajo sobre poliedros, mientras que Teón de Alejandría cita un comentario sobre la refracción de una obra perdida titulada Catoptrica. De esta forma siguiendo sus obras iremos desvelando, sus aportaciones a las matemáticas.

“Sobre el equilibrio de los planos“ en esta obra Arquímedes desarrollo la llamada Ley de la Palanca, en varfiuos postulados(teoría) y proposiciones (práctica):
Postulado 1: Pesos iguales a distancias iguales están en equilibrio y pesos iguales a distancias desiguales no están en equilibrio sino que se inclina (la palanca) hacia el peso que está a mayor distancia.
Se sobreentiende que las distancias se miden desde el fulcro o punto de apoyo de la palanca.

Postulado 2: Si, cuando los pesos ubicados a ciertas distancias están en equilibrio, se agrega algo a uno de los pesos ya no estarán en equilibrio, sino que desciende el lado donde se ha agregado peso.

Postulado 3: Análogamente, si algo se quita de uno de los pesos, ya no permanecerán en equilibrio y desciende el peso del que no se ha quitado nada.

En los postulados 2 y 3, se considera de manera implícita que todo es pesado y que la ligereza de un cuerpo no es otra cosa que la cualidad de ser menos pesado que otro cuerpo. Por otra parte, estos postulados resultan evidentes si nos imaginamos en la situación de estar realizando pesadas en una balanza de platillos de brazos iguales.

Postulado 4: Cuando figuras semejantes son iguales y se superponen una con la otra, sus centros de gravedad coinciden.

Postulado 5: En figuras semejantes que son desiguales, los centros de gravedad estarán similarmente situados. Por puntos análogos ubicados con relación a figuras semejantes, quiero decir puntos tales que si se trazan líneas rectas desde ellos con ángulos iguales, dichas líneas forman ángulos iguales con los correspondientes lados de las figuras.

Este postulado establece que figuras semejantes, es decir de la misma “forma”, pero desiguales, es decir de diferente tamaño, tendrán sus centros de gravedad en la misma posición “relativa”.

Postulado 6: Si magnitudes a ciertas distancias están en equilibrio, otras magnitudes iguales a ellas también estarán en equilibrio a las mismas distancias.

En este postulado, se plantea que a los efectos del equilibrio sólo son relevantes la magnitud y la distancia, con independencia de la forma o la sustancia. Es fundamental para la deducción de la ley de la palanca. Cuando Arquímedes dice “magnitudes iguales a otras magnitudes”, quiere decir “magnitudes del mismo peso”. Y cuando dice “magnitudes a ciertas distancias” quiere decir “los centros de gravedad de las magnitudes están a la misma distancia del fulcro” (Assis, 2008, p. 179).

Postulado 7: En cualquier figura cuyo perímetro es cóncavo en una y la misma dirección, el centro de gravedad debe estar dentro de la figura.

Con estos postulados, Arquímedes ha convertido un ámbito físico en una cuestión geométrica y, en el libro I deSobre el equilibrio de los planos, procede a demostrar rigurosamente siete proposiciones sobre el equilibrio.

Proposición 1: Pesos que se equilibran a iguales distancias son iguales.

Enuncia la inversa de la primera parte del Postulado 1, que se puede demostrar por el absurdo utilizando el Postulado 3. De acuerdo al Postulado 1 y a la Proposición 1, la igualdad de pesos y distancias es condición necesaria y suficiente del equilibrio.

Proposición 2: Pesos desiguales a distancias iguales no se equilibrarán sino que se inclinarán hacia el lado del peso mayor.

Proposición 3: Pesos desiguales se equilibran a distancias desiguales, el peso más grande estará a menor distancia que el peso más pequeño.

Proposición 4: Si dos pesos iguales no tienen el mismo centro de gravedad, el centro de gravedad de ambos tomados conjuntamente está en el punto medio de la línea que une sus centros de gravedad.

Proposición 5: Si tres magnitudes iguales tienen sus centros de gravedad sobre una línea recta a distancias iguales, el centro de gravedad del sistema coincidirá con el centro de gravedad de la magnitud ubicada en el punto medio.

Corolario 1: Lo mismo es verdad para cualquier número impar de magnitudes, si aquellas que están a iguales distancias del punto medio son iguales, mientras la distancia entres sus centros de gravedad sean iguales.

Corolario 2: Si hay un número par de magnitudes con sus centros de gravedad situados a iguales distancias sobre una línea recta y si las dos del medio son iguales, mientras que aquellas que equidistan entre si (a cada lado) son iguales respectivamente, el centro de gravedad del sistema es el punto medio de la línea que une los centros de gravedad de los dos del medio.

Con esta base Arquímedes usa los principios derivados para calcular las áreas y los centros de gravedad de varias figuras geométricas, incluyendo triángulos,paralelogramos y parábolas.

“Sobre la medida de un círculo” Arquímedes, trazo las medidas del circulo, en unas cartas enviadas a Dositeo, científico de Alejandría.
En el Teorema I de esa obra, Arquímedes nos ofrece una bella “cuadratura” del círculo con su método de exhaución; y en el Teorema III obtiene la famosísima aproximación del número π (¡la relación entre la longitud de una circunferencia y su diámetro!), la fracción 22/17. La enorme influencia que la obra arquimediana ejerció sobre la comunidad científica a lo largo de la Edad Media árabe y latina, así como en el Renacimiento italiano, tuvo en laMedida del círculo el representante más eficaz e iniciático, tanto por la fascinación de lo circular, como por la sencillez de los enunciados de sus teoremas y el magistral desarrollo de sus demostraciones.

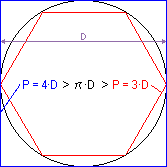
Arquímedes demostró que el lado del hexágono regular inscrito en un círculo es igual al radio de dicho círculo; así como que el lado del cuadrado circunscrito a un círculo es igual al diámetro de dicho círculo. De la primera proposición dedujo que el perímetro del hexágono inscrito era 3 veces el diámetro de la circunferencia, mientras que de la segunda dedujo que el perímetro del cuadrado circunscrito era 4 veces el diámetro de la circunferencia.

Afirmó además que toda línea cerrada envuelta por otra es de menor longitud que ésta, por lo que la circunferencia debía ser mayor que tres diámetros pero menor que cuatro. Por medio de sucesivas inscripciones y circunscripciones de polígonos regulares llegó a determinar el valor aproximado de π como:

\pi = {22 \over 7} = 3,142

Con los rudimentarios medios de los que disponía el sabio griego, el error absoluto que cometió en el cálculo de p resultó ser inferior a una milésima (0,0040 %).

cuadratura del circulo arquimedes

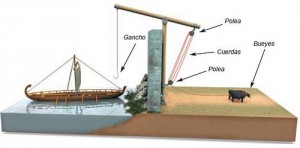
“Sobre las espirales” La espiral de Arquímedes (también espiral aritmética) obtuvo su nombre del matemático siciliano Arquímedes, quien vivió en el siglo III antes de Cristo. Se define como el lugar geométrico de un punto moviéndose a velocidad constante sobre una recta que gira sobre un punto de origen fijo a Velocidad Angular constante.

En coordenadas polares (r, θ) la espiral de Arquímedes puede ser descrita por la ecuación siguiente:

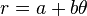
\, r=a+b\theta

siendo a y b números reales. Cuando el parámetro a cambia, la espiral gira, mientras que b controla la distancia en giros sucesivos.

Arquímedes describió esta espiral en su libro De las Espirales.

Esta curva se distingue de la espiral logarítmica por el hecho de que vueltas sucesivas de la misma tienen distancias de separación constantes (iguales a 2πb si θ es medido en radianes), mientras que en una espiral logarítmica la separación está dada por una progresión geométrica.
La espiral normal ocurre cuando x = 1.

Espiral de Arquímedes

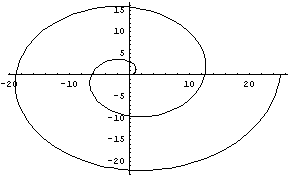
Otro ejemplo de espiral de Arquímedes

“Sobre la esfera y el cilindro” Se sabía calcular, al menos desde la época de los egipcios, el volumen de prismas y cilindros. Demócrito (~460 a.C. – 360 a.C.) demostró que el volumen de una pirámide es igual a la tercera parte del de un prisma de igual base y altura, e igual hizo con el cono respecto del cilindro. Euclides había demostrado en sus “Elementos” que el volumen de dos esferas es entre sí como los cubos de sus diámetros, o como diríamos actualmente, que el volumen de una esfera es proporcional a su diámetro. Arquímedes demostró, una vez más, que esa constante de proporcionalidad estaba muy relacionada con  pi. Una de los resultados más notables del libro es la

PROPOSICIÓN 33.- La superficie de cualquier esfera es cuatro veces la de su círculo máximo.
La demostración vuelve a ser una doble reducción al absurdo, suponiendo primero que la superficie de la esfera es mayor que cuatro veces la del circulo y suponiendo luego que es menor, llegando en ambos casos a una contradicción. La técnica empleada es el método de exhaución de Eudoxo; es decir, inscribiendo y circunscribiendo cuerpos geométricos, como conos y troncos de cono (cuyas superficies había demostrado previamente), y aproximándose desde dentro y desde fuera a la superficie de la esfera. Quedó establecido por lo tanto que S=4*pi*r2.

Quedaba sin embargo por demostrar otro de los resultados más importantes del libro,  la

PROPOSICIÓN 34.- Cualquier esfera es igual a cuatro veces el cono que tiene su base igual al círculo máximo de la esfera, y su altura igual al radio de la esfera.
La demostración la hace basándose en los volúmenes del cono y del cilindro que había hallado previamente. Partiendo de una esfera cualquiera, considera un cilindro cuyo radio de la base es igual al radio de la esfera y su altura igual al radio, y un cono con base igual a la del cilindro y altura igual al radio de la esfera. Haciendo un corte horizontal en los tres cuerpos a una altura inferior al radio, demuestra que la superficie de la sección correspondiente al cilindro es igual a la suma de las superficies de las secciones correspondientes al cono y a la esfera.

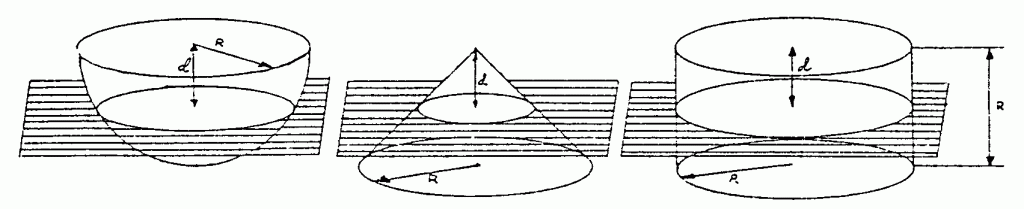
semiesfera

 

Si el corte lo hacemos a una distancia d del punto más alto de la figura, entonces el radio del circulo que aparece en la esfera es la raíz de R2-d2. El radio del circulo que aparece en el cono es d. En el cilindro el radio es R. Por tanto, pi*(R2-d2)+pi*d2=pi*R2.Lo que hoy conocemos como principio de Cavalieri implica que el volumen de media esfera más el volumen del cono es igual al volumen del cilindro. Como el volumen de este cilindro es pi*r3 y el del cono pi*r3/3, entonces tenemos que el volumen de la esfera completa es 4/3*pi*r3,

Como corolario de estos resultados obtiene que la relación entre una esfera y el cilindro que la contiene es 2:3, tanto en superficie como en volumen.

“Sobre los conoides y esferoides” Arquímedes examina paraboloides de revolución, hiperboloides de revolución, y esferoides obtenidos al rotar una elipse, ya sea, alrededor de su eje mayor, o de su eje menor.  El principal propósito de la obra es investigar el volumen de segmentos de estas figuras tridimensionales.

“Sobre los cuerpos flotantes” en el cual estudia científicamente el equilibrio de los cuerpos sumergidos y enuncia el que conocemos hoy com principio de Arquímedes, y que ya explicamos ayer, la anecdota o leyenda, que dice que lo descubrio en el baño, el principio dice así “Sobre todo cuerpo sumergido en un líquido actúa una fuerza hacia arriba (empuje) cuyo valor es igual al peso del líquido que ha desalojado”

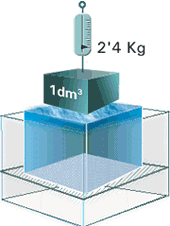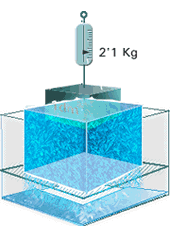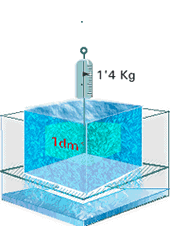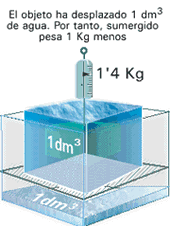
Ejemplo del principio de Arquimedes

“La cuadratura de la parábola” demuestra que: “Una sección de parábola excede en un tercio al área del triángulo de igual base que la sección y cuyo vértice es el de la parábola”. Dicho de otra forma, la superficie de la sección de parábola es igual a cuatro tercios de la superficie del triángulo inscrito. A partir de este resultado la cuadratura es obvia.

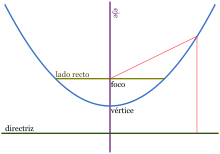
Partes de una parabola

“Ostomachion” En esta obra, cuyo tratado más completo que lo describe se encontró dentro del Palimpsesto de Arquímedes, Arquímedes presenta un rompecabezas de disección similar a un Tangram. Arquímedes calcula las áreas de 14 piezas que pueden ser ensambladas para formar un cuadrado. Una investigación publicada en 2003 por el Doctor Dr. Reviel Netz de la Universidad de Stanfordargumentaba que Arquímedes estaba intentando determinar en cuántas formas se podía ensamblar las piezas para formar un cuadrado. Según Netz, las piezas pueden formar un cuadrado de 17.152 maneras distintas. El número de disposiciones se reduce a 536 cuando se excluyen las soluciones que son equivalentes por rotación y reflexión. Este puzle representa un ejemplo temprano de un problema de combinatoria.

El origen del nombre del puzzle es incierto; se ha sugerido que puede haber surgido de la palabra griega para garganta, stómakhos(στόμαχος). Ausonio se refiere al puzzle como Ostomachion, una palabra griega compuesta por las raíces ὀστέον (osteon, ‘hueso’) y μάχη (machē, ‘lucha’). El puzzle es también conocido como el Loculus de Arquímedes o como la Caja de Arquímedes

Ostomachion

“El contador de arena” En este tratado, Arquímedes cuenta el número de granos de arena que entrarían en el universo. Este libro menciona la teoría heliocéntrica del Sistema solar propuesta por Aristarco de Samos, e ideas contemporáneas acerca del tamaño de la Tierra y las distancias de varios cuerpos celestes. Usando un sistema de números basado en la capacidad de la miríada, Arquímedes concluye que el número de granos de arena que se requerirían para llenar el universo sería de 8×1063, en notación moderna.

Para concluir con esta entrada, señalar dos curiosidades, como son “El método de teoremas mecánicos” carta dirigida a Eratósteles, y que se perdio en el olvido hasta el año 1907, cuando el matemático Heiberg, luego de copiar y examinar el escrito original junto con otros textos de Arquímedes que halló en la Biblioteca del Monasterio del Santo Sepulcro en Jerusalem, ubicada en Constantinopla, anuncia su descubrimento, este teorema consistía en Arquímedes emplea el cálculo infinitesimal, y muestra cómo el método de fraccionar una figura en un número infinito de partes infinitamente pequeñas puede ser usado para calcular su área o volumen. Arquímedes pudo haber considerado que este método carecía del suficiente rigor formal, por lo que utilizó también el método de exhausción para llegar a los resultados. Recordemos que el método de exhausción consiste en Este método consiste en considerar determinada magnitud de una figura, como el límite de las magnitudes correspondientes de figuras inscritas y circunscritas en ella, las cuales aproximan arbitrariamente la figura original.

Además Arquímedes como otros matemáticos planteo varios problemas matemáticos entre ellos el más famoso es el de “El problema del ganado de Arquímedes” que dice así “Si eres diligente y sabio, oh, extranjero, calcula el número de cabezas de ganado del Sol” tras varios estudios, de cuantas reses podía tener el dios Sol,  esta versión del problema fue resuelta por primera vez por A. Amthor en 1880 y la respuesta es un número muy grande, aproximadamente 7,760271×10206544.

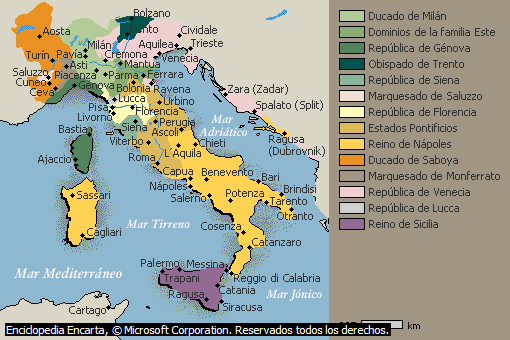
Hasta aquí, la vida de los grandes matemáticos de la edad antigua, que influyeron en el renacimiento italiano, y en concreto en Galileo Galilei

Posted in Sin categoría | Comments Off on Grandes matemáticos que influyeron en Galileo y en el pensamiento de la edad Moderna: Arquímedes y las Matemáticas (2ª Parte)

Grandes matemáticos que influyeron en Galileo y en el pensamiento de la edad Moderna: Arquímedes, Vida, Inventos y curiosidades (1ª Parte)

Posted on 2 junio, 2011 by sukicorleone

Arquímedes de Siracusa (ca. 287 a. C. – ca.212 a. C.)

Arquimedes

Considerado como el científico y matemático más importante de la Edad Antigua, y uno de los más grandes de toda la historia. Su padre Fidias fue astrónomo e influyó de forma notable en su educación. En aquella época, Alejandría estaba considerada como el centro de investigación y estudio más importante del mundo conocido. Arquímedes viajó hasta esta ciudad y estudió con los discípulos de Euclides, lo cual representó una influencia importante en su forma de entender las matemáticas. El resto de su vida la pasó en Siracusa, dedicado por completo a sus trabajos e investigaciones, donde murió según Plutarco en el año  212 a.C., cuando Siracusa fue tomada por los romanos después de un largo sitio, Arquímedes estaba resolviendo un problema en el suelo, cuando un soldado romano se acercó a él y le ordenó levantarse e irle a presentar sus respetos al general romano Marcelo. Arquímedes, muy molesto porque el soldado había pisado su dibujo, le gritó “No arruines mis esferas!” la reacción fue inmediata: el soldado lo mató. Marcelo, que había encargado explícitamente que no mataran a Arquímedes pues sabía de su fama de gran sabio, encargó que se le hiciera un funeral de honor.

Inventos
Se le atribuyen varios inventos a Arquimedes, pasaremos a repasar los más relevantes

Tornillo de Arquímedes: El tornillo de Arquímedes consiste simplemente en un enorme tirabuzón que gira accionado por una manivela situada en su parte superior. A veces, en lugar de la manivela, se colocaba directamente un molino, de manera tal que se utilizara la fuerza del viento para hacerlo funcionar.
El extremo inferior debe encontrarse sumergido en aquello que se desea levantar, generalmente agua, de modo tal que el tirabuzón quede inclinado con respecto a la superficie de lo que se desea elevar. Mientras el tirabuzón gira por acción de la manivela o del molino, una pequeña cantidad de agua queda atrapada dentro. La inclinación del Tornillo debe ser tal que parte del giro introduzca agua dentro del tirabuzón, y parte introduzca aire (para evitar un efecto sifón) el siguiente giro permitirá que más agua ingrese en él, y a su vez impedirá la salida de la que anteriormente había entrado. Cada porción de líquido queda atrapada en una sección del cilindro o tirabuzón que al girar la arrastra hacia arriba. De este modo, luego de sucesivos giros, el agua asciende poco a poco dentro del tornillo.

Dado que el objetivo era elevar el agua a una determinada altura (y no simplemente trasladarla desde un río a un campo), se solía usar más de un Tornillo en serie, debido a las limitaciones de la máquina. Así, el agua iba ascendiendo en etapas.

Tornillo de Arquímedes

La Garra de Arquimedes: La garra de Arquímedes es un arma que supuestamente fue diseñada por Arquímedes para defender la ciudad de Siracusa del asedio al que la habían sometido los romanos. También conocida como “el agitador de barcos”, la garra consistía en un brazo semejante a una grúa de donde estaba suspendido un enorme gancho de metal.. esta grua cuando los barcos se acercaban a las murallas de Siracusa, se accionaba, sujetando a los barcos, provocando graves daños a las naves enemigas e incluso su hundimiento.

La garra de Arquímedes

El rayo de calor de Arquímedes: Se cree que Arquímedes ideó una manera de utilizar la luz del sol para incendiar barcos, mediante la utilización de una gran cantidad de espejos enfocados en un mismo punto. De esta manera, se generaba una temperatura tan elevada que las embarcaciones comenzaban a arder. Cuenta la leyenda que al hallarse sitiado en Siracusa, por los romanos, Arquímedes utilizó el rayo de calor para repeler un ataque. Varios estudios han demostrado, mediante el uso de escudos de bronce como espejos, que para prender un barco de esta forma, se debían dar una serie de condiciones climatológicas muy específicas (cielo despejado, calor extremo) siendo mucho más facil el uso de flechas y catapultas.

Rayo de calor

Curiosidades

Anécdota de la palabra Eureka
Entre sus anécdotas más famosas se encuentra la famosa “Eureka”. Cuenta el arquitecto e ingeniero romano Vitruvio, que en cierta ocasión el rey Herón II de Siracusa ofreció una gran cantidad de oro a un orfebre, para que le hiciera una corona de oro totalmente pura. Cuando la corona estuvo terminada el rey comenzó a sospechar que el orfebre no había empleado todo el oro en la corona, y por tanto había sisado parte de él.

Herón II le planteó el problema a Arquímedes y éste se puso manos a la obra. Al no poder fundir la corona para calcular su masa y volumen, el problema se antojaba complicado. Sin embargo, mientras tomaba un baño, notó que el agua de la bañera se desplazaba cuando él se introducía en ella. De esta forma comprendió que si introducía un volumen dentro del agua y medía la altura que alcanzaba ésta, podría determinar el volumen de la corona y por tanto su densidad.

Imágen de Arquímedes, saliendo de la bañera en el momento del descubrimiento

Cuenta la historia que Arquímedes se puso tan contento al descubrir esto, que salió de la tina donde se estaba bañando y desnudo fue corriendo por las calles de la ciudad gritando: ¡Eureka! ¡Eureka! (en griego, “lo conseguí”). Cuando llegó al palacio, sumergió la misma cantidad de oro puro que el rey había entregado al orfebre y midió la altura del agua. Al introducir la corona notó como la altura era menor. De esta forma la única explicación era que las densidades eran diferentes. Finalmente el orfebre confesó que había quitado oro y agregado plata.

Punto de apoyo
Según otra anécdota famosa, recogida por Plutarco, entre otros, Arquímedes aseguró al tirano que, si le daban un punto de apoyo, conseguiría mover la Tierra; se cree que, exhortado por el rey a que pusiera en práctica su aseveración, logró sin esfuerzo aparente, mediante un complicado sistema de poleas, poner en movimiento un navío de tres mástiles con su carga.

Hasta aquí la primera parte de la vida de Arquímedes, en la próxima entrada, veremos los avances matemáticos que Arquímedes lego al mundo, y su importancia.

 

Posted in ciencia, Descubrimientos, Investigaciones | Comments Off on Grandes matemáticos que influyeron en Galileo y en el pensamiento de la edad Moderna: Arquímedes, Vida, Inventos y curiosidades (1ª Parte)

Grandes matemáticos que influyeron en Galileo y en el pensamiento de la edad Moderna: Pitágoras

Posted on 2 mayo, 2011 by sukicorleone

Como hablamos en anteriores post, Galileo Galilei se sintio profundamdente marcado por el pensamiento clásico, especialmente por Pitágoras y Arquimedes, es por ello, que creemos de especial relevancia, hablar de estos matemáticos para comprender mejor, los conocimientos de los que disponía Galileo, hoy hablaremos de Pitagoras (aproximadamente 582-507 a.C.) aunque hablar de Pitagoras, no es hablar exclusivamente de el, sino de toda su escuela, y sus discípulos, que hicieron varios descubrimientos de gran valor,  conocimientos que tuvieron gran calado entre los humanistas. Pasaremos pues a hacer una breve síntesis de estos importantes descubrimientos y de su filosofía.

Hizo varios descubrimientos de suma importancia, los más destacados son:

– Teorema de Pitágoras: El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Se saqbe que los egipcios y sirios lo usaban para sus construcciones, pero no lo habían enunciado, este teorema aun hoy en día se usa, para multiples utilidades como la arqueología.

Teorema de Pitágoras

Los números racionales: La escuela de Pitágoras, pensaba que los números eran perfectos, que expresaban el orden del universo, y por tanto todos eran números racionales, un número racional es un número que se puede escribir en fracción
(o sea, como un cociente).

Por ejemplo 1.5 es un número racional porque 1.5 = 3/2 (se puede escribir en forma de fracción)
Pero un discípulo de Pitágoras, Hipólito, encontró un numero que no puede ser racional, como es la Raíz cuadrada de 2, un numero irracional, es aquel que no se puede escribir en fracción, el decimal sigue para siempre sin repetirse, el más famosos es el número Pi, 3.1415926535897932384626433832795 (y más…)

Número pi

Según cuenta la leyenda Hipólito, fue tirado por la borda del barco, muriendo ahogado para que no contara que existían los números irracionales, y así terminar con la base de la doctrina filosófica de la escuela de Pitágoras, que adoraban al número como ente perfecto.

Clasificación de los números: La obsesión por los números y la adoración que les profesaban, condujeron a los pitagóricos a un estudio minucioso de los números. Establecieron diversas clasificaciones, entre otras la distinción entre pares e impares tal y como lo hacemos hoy, también otras más curiosas.
Números triangulares: Números naturales que se pueden expresar en forma de triangulo.

Números triangulares

Números cuadrados: Como los anteriores, pero estos se expresan en forma de cuadrados

Números cuadrados

Números perfectos: Son los números que son iguales a la suma de todos sus divisores excepto él mismo, por ejemplo, el 6 es un número perfecto puesto que 6=1+2+3

Los sólidos cósmicos: Sólo existen cinco poliedros regulares, que los pitagóricos veneraban y que llamaban sólidos cósmicos aunque fue Euclides el que demostró que no hay más poliedros regulares. Estas cinco figuras geométricas fueron admiradas, entre otros,  por Platón que pensó que representaban los elementos fundamentales que constituían el mundo: aire, fuego, agua, tierra y cosmos.

sólidos cósmicos

> Tetraedro, cuatro caras que son triángulos equiláteros. El fuego según Platón
> Cubo, seis caras que son cuadrados, Según Platón, La tierra
> Octaedro, ocho caras que son triángulos equiláteros, el aire, para Platón
> Dodecaedro, doce caras que son pentágonos regulares. Platón lo identifico con el cosmos.
> Icosaedro, veinte caras que son triángulos equiláteros. El agua para Platón

Estos podemos sintetizar que son los mayores descubrimientos de Pitágoras, en el campo de las matemáticas, pero Pitágoras, también intento dar su visión del cosmos, siempre basándose en la perfección de los números

Visión del Cosmos: Pitágoras combina los principios de Anaximandro y Anaxímenes para los cuales la realidad primordial es el pneuma ilimitado, el cual constituye el ser y fuera del cual existe el no ser, el vacío o el espacio.
El cosmos está formado por el pneuma ilimitado, es uno, sin partes, compacto pero limitado. Las cosas se formaron por el movimiento eterno que hay en el ser. Este cosmos limitado comenzó a respirar y en el aire que respira recibió el ser y el no ser, de este modo se rompió su unidad y comenzó a disgregarse dando origen a la multiplicidad a la pluralidad numérica, el mundo está lleno de contrarios, por lo que se necesita un elemento que coordine esas oposiciones. Ese elemento es la armonía.
Dentro del pneuma ilimitado, agitado por el movimiento eterno, se formo un cosmos esférico, limitado lleno, compacto sin distinción de partes. Este cosmos es el uno, la mónada, lo impar y constituye el principio de la unidad. El cosmos es una esfera viviente dotada de respiración y al respirar inhalo el pneuma ilimitado y el vacío, los cuales penetraron en si interior disgregando su unidad. Con ello se origina la pluralidad numérica de las cosas, cada una de las cuales es igual a una unidad o a un número. El vacío o el espacio sirven para disgregar la unidad primitiva del cosmos esférico y compacto y para determinar la naturaleza de las cosas, limitándolas y situándolas en distintos lugares y haciendo posible el movimiento.

busto de Pitágoras

Así podemos sintetizar la ciencia y la filosofía de Pitágoras, para saber más sobre él, acudan a la sección de enlaces, donde podrán encontrar mayor información

Posted in ciencia, Descubrimientos, Investigaciones | Comments Off on Grandes matemáticos que influyeron en Galileo y en el pensamiento de la edad Moderna: Pitágoras