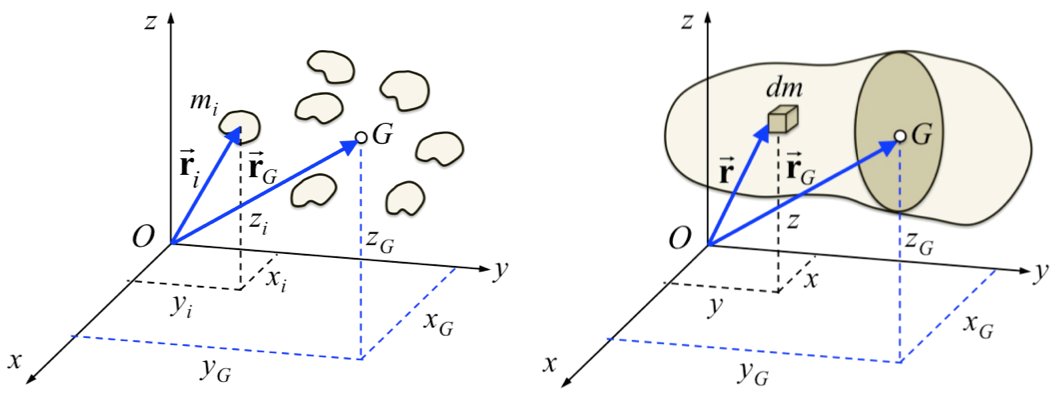
En muchos problemas relacionados con la estática y la dinámica del sólido rígido aparecen unas magnitudes denominadas centros de gravedad y momentos de inercia que están relacionadas con la forma en la que está la masa distribuida geométricamente en el espacio. Por esta razón, estas magnitudes se engloban en lo que se denomina geometría de masas.
Si consideramos el movimiento plano de un sólido rígido, éste tiene un tamaño y una forma definidos, por lo que un sistema de fuerzas no concurrentes puede hacer que el cuerpo se traslade y rote.
La traslación está regida por la segunda ley de Newton F = ma. Los aspectos de rotación provocados por un momento M están regidos por una ecuación de la forma M = Iα en la que α es la aceleración angular, mientras que I es el momento de inercia de masa. Por comparación, el momento de inercia mide la resistencia del cuerpo a la aceleración angular (M = Iα) del mismo modo que la masa mide la resistencia de un cuerpo a la aceleración (F = ma).
En este tema se verán los métodos utilizados para determinar la posición del centro de gravedad así como el momento de inercia de un cuerpo.