Tag Archives: aplicaciones

La importancia de transmitir y analizar bien los datos estadísticos, un ejemplo sobre política

Posted on by

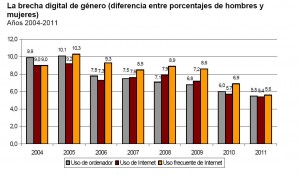
Estos últimos días he leído estas dos afirmaciones  en distintos medios de comunicación y blogs atribuidas al ministro de Educación Wert. No he podido contrastar qué dijo exactamente ya que no he encontrado el vídeo con las palabras exactas pero todo parece apuntar  que fue la segunda. Lo que sí he constatado es que el ministro suele basarse mucho en datos estadísticos para justificar reformas, comisiones de expertos y recortes. Pero hay que tener cuidado a la hora de transmitir datos estadísticos  ya que si el análisis previo  no es exhaustivo  la información que nos llega puede llenar titulares y darnos a entender a la sociedad cosas (en este caso ha sido sobre el sistema universitario) que realmente no son las que concluyen los datos estadísticos.

Las afirmaciones leídas  son:

(1)        Hay un 21% de desempleo entre los universitarios de 25 a 29 años.

(2)        Entre los parados de 25 a 29 años, el 21% son universitarios.

Muchas personas tienden a pensar que se está diciendo lo mismo en ambos casos pero ni mucho menos. Veámoslo:

(1)        Si se indica que hay un 21% de desempleo entre los universitarios de 25 a 29 años nos están diciendo que el porcentaje de parados en el conjunto de los universitarios entre 25 y 29 años es del 21%.

Vamos a plantearlo en forma de probabilidades condicionadas tal y como vimos en las clases de estadística:

P(estar parado| ser universitario entre 25 y 29 años)=0.21.

Si esto fuera cierto, es un dato muy  alarmante pero en un análisis estadístico serio que permitiera analizar realmente la situación se deberían haber incluido datos adicionales tales como el porcentaje de parados en  el conjunto de personas  no universitarias de 25 a 29 años o el porcentaje de parados en el conjunto de jóvenes en general de 25 a 29 años.

Estos porcentajes tratados como probabilidades (tanto por uno) corresponderían   con calcular las siguientes probabilidades condicionadas, respectivamente:

P(estar parado| no ser universitario y tener entre 25 y 29 años)

P(estar parado| tener entre 25 y 29 años)

Estas probabilidades no se pueden obtener del dato inicial (21%) ya que los conjuntos de referencia para los que se calcula la cantidad de parados son diferentes en cada uno de los tres casos.

Ya puestos, si se quiere hacer un estudio estadístico serio, se podrían realizar contrastes de hipótesis sobre proporciones y análisis ji-cuadrado para obtener unas primeras aproximaciones para el  total de la población que permitiera analizar el panorama actual de forma más fiable. No olvidemos que la mayoría de estas estimaciones estadísticas se obtienen a partir de muestras aleatorias, es decir con subconjuntos aleatorios de la población y no con toda la población. La inferencia estadística es la que permite extraer conclusiones para la población a partir de los datos muestrales.

(2)        En el segundo caso se dice: entre los parados de 25 a 29 años, el 21%  son universitarios.  La comprensión de esta afirmación es sencilla: concretamente nos están diciendo  que la población parada entre 25 y 29 años está distribuida de la siguiente forma: un 21% son universitarios y por tanto un 79% son no universitarios.  Si lo tratamos en términos de probabilidades diríamos:

P(ser universitario| ser parado con edad entre 25 y 29 años)=0.21.

Y como la probabilidad de un suceso es igual a uno menos la de su complementario obtenemos:

P(no ser universitario| ser parado con edad entre 25 y 29 años)=1-P( ser universitario| ser parado con edad entre 25 y 29 años)=1-0.21=0.79

Aunque a priori parezca dar mucha información, no es así,  y no son las probabilidades condicionadas más útiles para estudiar el problema del paro que nos ocupa. Para intentar analizar estadísticamente dicha afirmación deberíamos además  saber al menos qué porcentaje de universitarios y no universitarios hay en el conjunto de todos los jóvenes de 25 a 29 años y qué porcentaje de universitarios y no universitarios hay en el conjunto de todos los jóvenes de  25 a 29 años no parados.

En Facebook he compartido también un enlace a un artículo de José Antonio Pérez y Juan Hernández en el que los autores  muestran cómo el planteamiento que hace  Wert para justificar la reforma universitaria tiene datos estadísticos tratados  erróneamente.

No lo olvidéis, para hablar de estadística se ha de hacer con rigurosidad, no sirve con utilizar sólo aquellos datos estadísticos que van a ser favorables o convenientes  a unos propósitos  obviando otros que realmente permitirían radiografiar de forma más completa y real el sistema universitario español.

Medición de audiencias en Internet

Posted on by

En los siguientes vídeos de la asignatura seguimos tratando  la  medición de audiencias. En este caso tratamos la medición de audiencias en Internet.

Vídeo 1: Metodología user-centric.

Vídeo 2: Metodología site-centric.

Ahora le toca el turno a la medición de audiencias en televisión

Posted on by

En el siguiente vídeo de la asignatura seguimos tratando  la  medición de audiencias. En este caso tratamos los parámetros básicos de interés en la medición de audiencias en televisión.

En el vídeo se habla muy de pasada  de los audímetros, si quieres saber algo más sobre ellos  y cómo funcionan te recomiendo que vayas a la siguiente entrada del blog: ¿Qué es un audímetro? ¿Has visto alguna vez uno?

 

Seguimos con medición de audiencias en prensa

Posted on by

En el siguiente vídeo de la asignatura seguimos tratando  la  medición de audiencias. En este caso tratamos los parámetros básicos de interés en la medición de audiencias en prensa.

En el vídeo anterior se habla del Estudio General de Medios (EGM), si quieres saber más sobre el mismo accede a la siguiente página web: ¿Qué es el EGM?

Resultados de la encuesta sobre equipamiento y uso de TICs en los hogares – 2011

Posted on by

Los resultados de la encuesta realizada por el INE (Instituto Nacional de Estadística) revela que el 61,9% de los hogares disponen de  conexión de banda ancha a Internet. Esta cifra  ha aumentado un 9,3% respecto al año 2010. También sigue creciendo el porcentaje de internautas, un 4,5% más. Además, cabe destacar que la brecha digital de género (es decir, la diferencia de puntos entre sexos respecto a los principales indicadores de uso de TIC) volvió a reducirse en 2011, manteniendo así la tendencia de los últimos años. Esta brecha digital disminuyó en los principales indicadores analizados (uso de ordenador y de Internet y uso frecuente del mismo):


La encuesta ha investigado por primera vez la participación en redes sociales. El 52,3% de los usuarios de Internet en los últimos tres meses participa en redes sociales de carácter general, como Facebook o Twitter, creando un perfil de usuario o enviando mensajes u otras contribuciones. Los más participativos son los estudiantes (90,2%) y los jóvenes de 16 a 24 años (88,5%). Por sexo, las mujeres participan más que los hombres (54,8% frente al 49,9%). Por otra parte, el 10,4% de los internautas en los últimos tres meses ha participado en redes de tipo profesional, como LinkedIn o Xing. Este porcentaje se eleva al 27,2% en los trabajadores relacionados con el sector TIC y alcanza al 17,7% en los titulados superiores.

Leer nota de prensa completa

Llamar, madrugar y, si acaso, navegar

Posted on by

Según un estudio de la Universidad de Alicante, los estudiantes de la provincia utilizan más los servicios básicos de los móviles que las tecnologías de última generación de los terminales. Como era lógico los servicios más utilizados son hacer y recibir llamadas y mandar y recibir mensajes. Pero de la muestra de 3317 estudiantes encuestados parece ser que  una gran mayoría (86.2 por ciento) también lo usa como despertador.  El tema de chatear o navegar por Internet está menos extendido ya que sólo el 35.4 por ciento  del alumnado se conecta a la red con el móvil y sólo  algo más de la mitad de esta minoría tiene tarifa plana de datos. Si comparamos los resultados obtenidos para hombres y mujeres, ellos navegan más (el 49 por ciento)  que ellas (el 30 por ciento).

Leer noticia completa en El Información

Un estudio matemático predice un 50% de aumento de los divorcios en cinco años

Posted on by

Las matemáticas dibujan un futuro complicado al matrimonio. Para llegar a esta conclusión, un equipo de investigadores del Instituto Universitario de Matemática Multidisciplinar de la Universidad Politécnica de Valencia han desarrollado un modelo matemático de sistemas de ecuaciones lineales y cuadráticas que toman como referencia los datos de las encuestas realizadas por el Instituto Nacional de Estadística (INE).

Leer noticia completa en el País.

La industria del videojuego es la primera industria de ocio audiovisual e interactivo de España, con una cuota de mercado que supera el 50 por ciento

Posted on by

Así se desprende del informe elaborado por aDeSe (Asociación Española de Distribuidores y Editores de Software de Entretenimiento). El anuario 2010, presentado por la asociación este mes de julio, recoge  información sobre  el sector del videojuego y el estado de su industria, tanto en nuestro país como en los principales mercados internacionales. Se puede consultar, entre otros aspectos, información económica sobre el mercado español del videojuego, el contexto regulador que rodea a la industria, estadísticas sobre el consumo en los principales mercados internacionales, información detallada sobre el perfil del videojugador español y europeo, estudios de mercado sobre el futuro de la industria, etc. Asimismo, el documento recoge un recopilatorio de los lanzamientos más importantes en el mercado español, el ranking de ventas durante el año, la visión sobre la industria de los máximos directivos de las empresas de videojuegos que operan en el mercado español y un resumen de las citas más importantes del año para el sector.

Leer noticia completa  en aDeSe.

¿Qué es el INE?

Posted on by

El Instituto Nacional de Estadística (http://www.ine.es/) tiene como misión la elaboración y perfeccionamiento de las estadísticas demográficas, económicas y sociales ya existentes, la creación de otras nuevas y la coordinación con los servicios estadísticos de las áreas provinciales y municipales.

INEbase es el sistema que utiliza el INE para el almacenamiento de la información estadística en Internet. Contiene toda la información que el INE produce en formatos electrónicos.

A las operaciones estadísticas se puede acceder directamente a través de la lista completa de operaciones de INEbase o a través de los menús temáticos. Estos menús permiten conocer toda la información disponible de cada tema: operaciones para las que se presentan resultados, junto con una pequeña descripción de las variables publicadas, la periodicidad y disponibilidad de los datos y el ámbito geográfico; publicaciones y estudios relacionados; enlaces a otras webs donde ampliar la información de fuentes externas; y un enlace al Inventario de Operaciones Estadísticas de la Administración General del Estado (IOE) para conocer todas las operaciones del Sistema Estadístico Español relacionadas con el tema.

Para cada operación estadística en INEbase existe una página que da acceso a toda la información relativa a la misma: los resultados detallados completos, la última nota de prensa publicada, el calendario de disponibilidad de datos y toda la información metodológica o descriptiva que ayuda a la mejor comprensión e interpretación de los datos (metodologías, cuestionarios, clasificaciones, notas explicativas,…).

Los resultados detallados incluyen los últimos resultados publicados y además la historia reciente de la estadística. Los ficheros de datos se pueden visualizar directamente desde INEbase o descargar  en diversos formatos (excel, csv) incluido el formato  Pc-Axis para un tratamiento posterior utilizando el programa Pc-Axis cuya descarga se puede hacer de forma gratuita.

Estadística y sondeos electorales

Posted on by

En breve habrá elecciones municipales en España y ya han empezado a realizarse los primeros sondeos.  Los sondeos electorales son una de las aplicaciones de la estadística que más interés despierta. Una de las características de estos sondeos  es que una vez realizadas las elecciones se sabe si las estimaciones obtenidas con las encuestas se han acercado realmente a los resultados definitivos obtenidos en las elecciones. Por lo que todos podemos opinar y como la realidad es que algunas veces fallan, esto produce críticas e incredulidad dando la impresión de que la estadística no es una ciencia seria. Pero no siempre es así, muchos han sido los casos de éxito a lo largo de la historia electoral.

Quizá deberíamos hacernos la siguiente pregunta: ¿Se aplican bien los principios de la  estadística matemática?

  • Para que los resultados obtenidos se puedan extrapolar a la población es imprescindible que la muestra sea realmente representativa de la población y se haya obtenido de forma aleatoria.
  • Los sondeos electorales se basan en encuestas realizadas con anterioridad a las elecciones y todos sabemos que la intención de voto va cambiando. Dichos cambios no se pueden predecir  estadísticamente. Un ejemplo claro de este aspecto lo tenemos en lo que ocurrió en las elecciones españolas de 2004, cuando tres días antes de las elecciones se produjo el atentado del 11 de marzo. En este caso, los sondeos electorales fracasaron estrepitosamente.
  • No se puede saber a quién votarán los indecisos. El grupo de indecisos suele representar entre el 20% y 50% y en  estos sondeos, atendiendo  a las respuestas a una serie de preguntas adicionales (como   a qué partido votó en las últimas elecciones o con qué partido simpatiza)  se toma la decisión de asignar cada uno de esos votos indecisos  a uno u otro partido. Esto no tiene nada que ver realmente con la estadística, sino más bien con la sociología, psicología y el análisis político.
  • Nadie nos asegura que los encuestados hayan sido sinceros en su respuesta.
  • En unas elecciones lo relevante no es el porcentaje de votos que va a tener cada partido, sino el número de escaños. Como se ha visto en el vídeo, en España se usa la ley d’Hondt. Toda encuesta estadística tiene un error, en este caso del 3.01% con una confianza del 95% (este concepto, aunque queda bastante claro en el vídeo, se tratará en el tema 6). Ese error puede decantar un escaño a un partido u otro, pero no se tiene información suficiente para tomar la decisión a priori.

¿Qué es un audímetro? ¿Has visto alguna vez uno?

Posted on by

Si quieres saber algo más sobre los sistemas de medición de audiencias en televisión y esos aparatitos que se llaman audímetros que explicamos en clase puedes ver el siguiente  reportaje: como verás alrededor de 4.500 familias (4.625 hogares, a día de hoy, según la información disponible en la página web de Kantar Media) en España deciden lo que vemos todos por la tele. Y nadie sabe quiénes son.

La llegada de la tecnología digital supuso un serio problema para los audímetros tradicionales. Se ponía en cuestión su principal capacidad: el reconocimiento preciso de la cadena sintonizada. Tal reconocimiento se hacía a través de la detección de la frecuencia de sintonía o del canal radioeléctrico. La correspondencia entre canal radioléctrico y cadena era biunívoca para un dispositivo determinado, con lo que la base para la determinación de la cadena estaba establecida. El problema es que en un entorno digital, dentro de un mismo canal radioeléctrico se concentran las señales de un número diverso de cadenas diferentes. Una de las soluciones para este problema ha sido utilizar un enfoque basado en el  reconocimiento de la señal de vídeo. Es la línea que sigue, entre otros, el Picture Matching System que actualmente utiliza Sofres AM (actualmente Kantar Media) para la identificación de las cadenas emitidas por las plataformas digitales en España.

El audímetro Picture Matching basa su funcionamiento en el contenido de la emisión en sí, más concretamente en la señal de vídeo, es decir, en la imagen que se está viendo en el televisor sondado. La filosofía general consiste en el almacenamiento de muestras de la señal de vídeo en los televisores de los hogares que, tras su comparación (matching) con las muestras tomadas para cada una de las cadenas, permitirá determinar cual es la cadena vista en un televisor en cada momento.

Lo que realmente recoge el audímetro no son muestras de la imagen, sino el resultado de múltiples comparaciones de luminosidad entre pares de parcelas o celdas de la pantalla. Para el Picture Matching, la imagen se reduce a la luminosidad media de 32 pequeñas celdas que se encuentran fijadas de forma pseudo-aleatoria en la pantalla.

Estas 32 celdas están organizadas en 16 parejas, de cada una de las cuales se pueden obtener dos posibles resultados dependiendo de cual de las dos parcelas que forman dicha pareja sea más oscura. Tendremos por tanto 16 bits de información posible por cada imagen en la pantalla, (un bit por pareja, si la celda de la izquierda es más oscura que la de la derecha, le asignará el valor “1”, en caso contrario le asignara el valor “0”). La superficie de la imagen con la que el audímetro opera supone aproximadamente un 5 % de la superficie total de la pantalla.

El sistema sigue un algoritmo de eliminación, es decir, determina la cadena correspondiente por eliminación de aquellas que no lo son. Al comenzar el proceso, se contemplan todas las cadenas controladas y se van comparando las muestras (bits) recogidas en el hogar con las obtenidas en la Central para cada una de las cadenas. A medida que se producen discordancias entre la información de una cadena y la obtenida en el hogar, esta cadena es eliminada, y se continúa la comparación con las cadenas restantes. Cuando, durante el proceso, solo quede una cadena para la cual los datos de la Central y del hogar sean coincidentes, ésta será la cadena vista en dicho televisor. Cuando estos datos dejan de coincidir es señal de que se ha producido un cambio de cadena, incluyéndose de nuevo todas las cadenas para realizar una vez más el proceso de eliminación.