Aquí os dejo un ejercicio para comprobar si tenéis claros los distintos tipos de variables. Se ha utilizado la plataforma educaplay.
Tag Archives: ejercicios
Cuatro ejercicios sobre probabilidad, cuatro soluciones …
Aquí os dejo unos ejercicios resueltos para practicar algunos conceptos de probabilidad.
http://www.slideshare.net/violetamigallon/cuatro-ejercicios-probabilidad
¿Cuántos números de 6 cifras …?
¿Te atreves con el siguiente ejercicio?:
¿Cuántos números no negativos de seis cifras tienen al menos una cifra par?
Ayúdate de la siguiente actividad tipo test para ver si sabes plantear este tipo de problemas. Hay preguntas de respuesta única y de respuesta múltiple:
Enunciados de ejercicios relacionados con las distribuciones continuas
Ejercicio 1. Sea X una variable aleatoria continua tal que:
f(x)=1/x2, x>1
f(x)=0, en el resto
Comprueba que f cumple las propiedades para ser una función de densidad. Calcula la función de distribución de X. Obtén k tal que F(k)=1/2.
Ejercicio 2. Sea X una variable aleatoria continua cuya función de densidad es
f(x)=x, 0≤x≤1
f(x)=2-x, 1<x≤2
f(x)=0, en el resto
Calcula su función de distribución.
Ejercicio 3. Calcula el valor de k para que la siguiente función sea la función de densidad de una variable aleatoria continua X.
f(x)=k(1-x)2, 0<x<1
f(x)=0, en el resto
Una vez obtenido k, calcula la función de distribución de X.
Ejercicio 4. Sea X una variable aleatoria continua cuya función de densidad es
f(x)=1/3, 0<x<3
f(x)=0, en el resto
Calcula E(X) y Var(X).
Ejercicio 5. Calcula el valor de k para que la siguiente función sea la función de densidad de una variable aleatoria continua X.
f(x)=ke-x/2, x>0
f(x)=0, en el resto
Ejercicio 6. Sea X una variable aleatoria continua cuya función de densidad es
f(x)=1-|x|, |x|<1
f(x)=0, en el resto
Calcula su función de distribución.
Ejercicio 7. Calcula el valor de k para que la siguiente función sea la función de densidad de una variable aleatoria continua X.
f(x)=kx2, -3<x<6
f(x)=0, en el resto
Una vez obtenido k, calcula P(X>2), sin calcular previamente la función de distribución.
Ejercicio 8. Calcula el valor de k para que la siguiente función sea la función de densidad de una variable aleatoria continua X.
f(x)=kx(1-x), 0<x<1
f(x)=0, en el resto
Una vez obtenido k, calcula P(X>0.5), sin calcular previamente la función de distribución.
Ejercicio 9. Sea X una variable aleatoria continua cuya función de densidad es
f(x)=2/3, 0<x<1
f(x)=1/3, 1≤x<2
f(x)=0, en el resto
Calcula E(X) y Var(X).
Ejercicio 10. Calcula el valor de k para que la siguiente función sea la función de densidad de una variable aleatoria continua X.
f(x)=k(1-x), 0≤x≤1
f(x)=0, en el resto
Una vez obtenido k, obtén la función de distribución. Calcula P(X<1/2), P(X>0.8) y P(X>1/4| X<1/2). Calcula E(X) y Var(X).
Otra actividad sobre teorema de Bayes y probabilidad total
Esta actividad se propuso en las actividades voluntarias del curso 2011-2012. Cayó también en un control del curso anterior.
Pincha en la imagen de la entrada si deseas realizar la actividad desde la web de educaplay.
¿Sabes resolver los ejercicios de análisis combinatorio de las actividades del tema 4? Compruébalo con la siguiente actividad
Con la realización de las siguientes actividades podréis analizar si sabéis resolver ejercicios sencillos de análisis combinatorio. Pincha en la imagen de la entrada si deseas realizar la actividad desde la web de educaplay o imprimir los enunciados de los ejercicios.
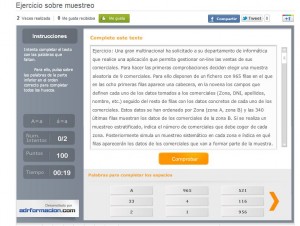
Ejercicio sobre muestreo estratificado, obteniendo las muestras de cada estrato mediante muestreo sistemático
Con la realización de la siguiente actividad podéis profundizar en la forma de realizar un muestreo estratificado en el que la muestra de cada estrato se obtiene por un muestreo sistemático. Este ejercicio se puso en un control del curso 2010-2011.
Análisis inferencial de datos categóricos con SPSS
El siguiente vídeo resume algunas de las opciones del SPSS que se van a utilizar en el tema 8 (Análisis inferencial de datos categóricos) para realizar la correspondiente práctica en el laboratorio.
Ejercicio sobre intervalos de confianza
Os adjunto un ejemplo de cálculo de intervalo de confianza, en el que se incluyen los distintos pasos a seguir para llegar a la solución. Os puede servir de ayuda a la hora de realizar la práctica relativa al tema 6.
Distribución Binomial con Geogebra
En el siguiente enlace encontraréis otro geogebra de Manuel Sada. Esta vez está dedicado a la distribución binomial, el cálculo de la función de cuantía y conceptos relacionados.
Distribución Binomial B(n,p) y cálculo de probabilidades en dicha variable aleatoria discreta.
Distribución binomial: un ejemplo de cálculo de probabilidades
En este curso, para resolver problemas relacionados con la distribución binomial se utiliza el SPSS. Por ejemplo, supongamos que un examen consta de 10 preguntas con 2 posibles respuestas cada una, de las cuales solamente una es correcta. Si se responde al azar a cada una de las preguntas, hay que calcular una serie de probabilidades.
a) Probabilidad de acertar 5 preguntas exactamente.
b) Probabilidad de acertar al menos 1.
c) Probabilidad de acertar al menos 5.
d) Probabilidad de contestar correctamente entre 3 y 6 preguntas en dicho test.
Solución:
Sea X=número de preguntas contestadas correctamente en un test de un total de 10 preguntas.
n=10
p=p(éxito)=p(pregunta contestada correctamente)=0.5, por tanto p permanece constante.
Asumiendo independencia entre las contestaciones de las preguntas, obtenemos que X~B(10,0.5).
Entonces:
a) P(X=5)=PDF.BINOM(5,10,0.5).
b) P(X≥1)=1-P(X<1)=1-P(X=0)=1-PDF.BINOM(0,10,0.5).
c) P(X≥5)=1-P(X<5)=1-P(X≤4)=1-CDF.BINOM(4,10,0.5).
d) P(3≤X≤6)=P(X≤6)-P(X<3)=P(X≤6)-P(X≤2)=
=CDF.BINOM(6,10,0.5)-CDF.BINOM(2,10,0.5)=0.773437.
Ahora solamente quedaría acceder al SPSS y hacer los cálculos oportunos. Recordad que a la hora de corregir los ejercicios se le dará mucha importancia al planteamiento, el cual se debe realizar de forma razonada e incluyendo todos los pasos como se ha hecho aquí.