Category: Problems

Categories
Aims Problems Subject

Chapter 11: Structural members – Beams – Problems

After reading previous entry and understanding the meaning of isostatic beam, shear force, bending moment, how to apply method of sections, you should try to solve next exercises.

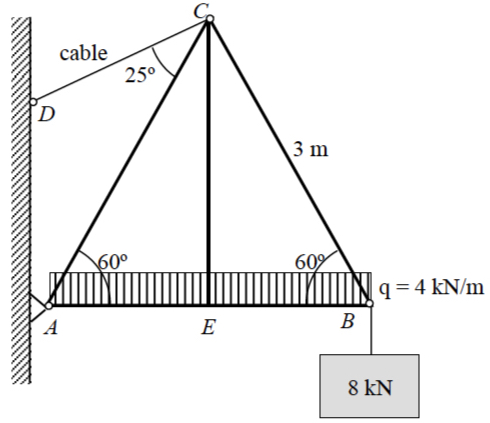
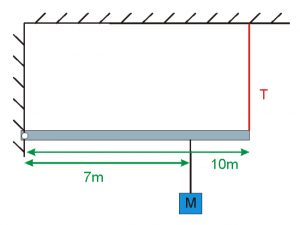
EXERCISE 1: A cantilever beam AB with mass 100 kg is subjected by cables as shown in figure. If the moment acting on the beam at A is greater than 2400 kN·m, beam will give way at A.

a) Determine the maximum weight of the load suspended by the two cables.

b) Draw shear and moment diagrams specifying values at all change of loading positions and at points of zero shear.

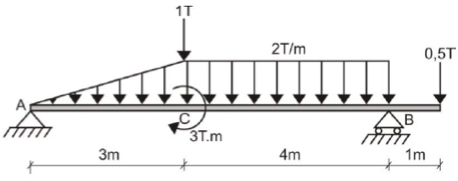
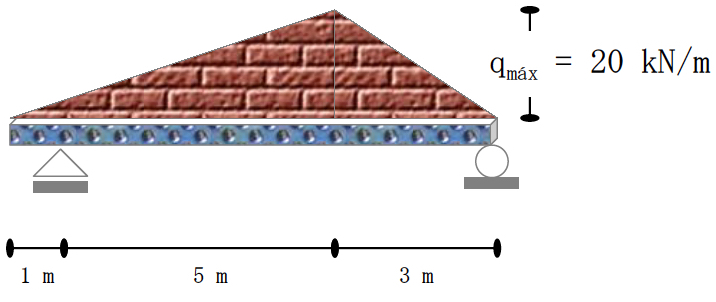
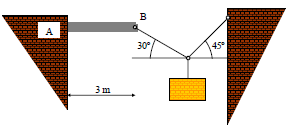EXERCISE 2: Draw the shear-force and bending-moment diagrams for the loaded beam and determine the maximum moment M and its location x from the left end.

Categories
Aims Problems Subject

Chapter 9: Elasticity – Problems

After reading previous entry and understanding the meaning of stress and strain, how to apply Hooke’s law to elastic solids, you should try to solve next exercises.

EXERCISE 1: A steel wire has a length of 25 m and its cross-sectional area is 6 mm × 0.8 mm. Considering the effect of its own weight negligible, calculate the strain and the change in length when we applied a tension force of 6 kp. Young’s modulus of steel is 2.1×10^6 kp/cm^2.

EXERCISE 2: Determine the elongation of a bar of uniform cross section S and length L which is hanging and subjected to its own weight.

 

Categories
Aims Problems Subject

Chapter 6: Equilibrium of rigid bodies (III). Distributed forces – Problems

After reading previous entry and understanding the meaning of distributed forces, how to calculate the equivalent resultant to the distributed load, you should try to solve next exercises.

EXERCISE 1: Calculate the supports reactions at A and B for the beam subjected to the asymmetric load distributions.

EXERCISE 2: The symmetric simple truss is loaded as shown. Determine the reactions at wall support A and the tension in cable CD.

Categories
Aims Problems Subject

Chapter 6: Equilibrium of rigid bodies (II). Stability – Problem

After reading previous entry and understanding the meaning of stability, rollover and stabilising moments, you should try to solve next exercise.

A homogeneous cylinder of radius R has a cylindrical hole of diameter R as shows in Figure. Cylinder can roll down the inclined plane without slipping. Determine the maximum angle θ of the inclined plane because the cylinder be in equilibrium. Obtain also the angle between the horizontal and the diameter AB in this situation.

NOTE: you can send your solution by tutorial tool in UACloud for including it in the continuous evaluation.

Categories
Aims Problems Subject

Chapter 4: Rigid bodies. (III) – Problems

ROTATIONAL DYNAMICS: EXERCISES

  1. A mass M = 120 kg hangs from a beam which is held by a cable.
    1. What is the tension T in the cable?
    2. Does the wall exert any force on the beam? Which one?
  2. A stone of mass 0.6 kg is forced to travel in a circle while it hangs from the ceiling, as shown in Figure. If the angle between the rope and the vertical is θ = 30º and the radius of the circle is r = 35 cm:
    1. What is the speed of the stone?
    2. What is the tension in the rope?
  3. A wheel of radius r = 80 cm has moment of inertia 10 kg m2. It is rotating around its central axis propelled by a rocket attached to a point on its outer rim. The rocket is expelling gas
    tangentially to the wheel, resulting in a constant force. Determine:

    1. The magnitude of the equivalent force, if we know that the wheel, starting from rest, reaches an angular speed of 1 rev/s in 6 s.
    2. The value of both tangential and normal acceleration in a point on the outer rim of the wheel.
    3. The angle that the total acceleration forms with the radius at that point.
    4. The time that the wheel takes to reach the same angular velocity, under the action of the same force, if we add a very thin ring of mass 5 kg around the outer rim.