DISTRIBUTED FORCES
In the previous sections we treated all forces as concentrated along
their lines of action and at their points of application. This treatment provided a reasonable model for those forces. Actually, “concentrated” forces do not exist in the exact sense, since every external force applied mechanically to a body is distributed over a finite contact area, however small.
What is more, distributed forces are a particular case of a coplanar parallel system of forces. The body force due to the gravitational attraction of the earth (weight) is by far the most commonly encountered distributed force. Figure shows (Meriam & Kreige 7th edition):
- Line distribution: When a force is distributed along a line, as in the continuous vertical load supported by a suspended cable, Fig. (a), the intensity w of the loading is expressed as force per unit length of line, newtons per metre (N/m).
- Area distribution: When a force is distributed over an area, as with the hydraulic pressure of water against the inner face of a section of dam, Fig. (b), the intensity is expressed as force per unit area. This intensity is called pressure for the action of fluid forces and stress for the internal distribution of forces in solids. The basic unit for pressure or stress in SI is the newton per square meter (N/m2), which is also called the pascal (Pa).
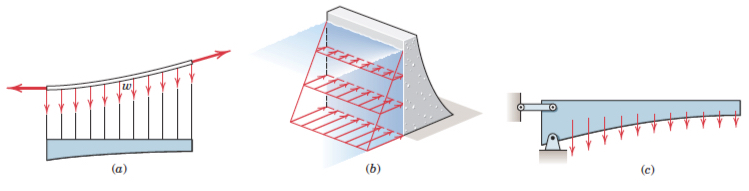
- Volume distribution: A force which is distributed over the volume of a body is called a body force. The most common body force is the force of gravitational attraction, which acts on all elements of mass in a body. The determination of the forces on the supports of the heavy cantilevered structure in Fig. (c), for example, would require accounting for the distribution of gravitational force throughout the structure. The intensity of gravitational force is the specific weight ρg, where is the density (mass per unit volume) and g is the acceleration due to gravity. The units for ρg are (kg/m3)(m/s2) N/m3 in SI units
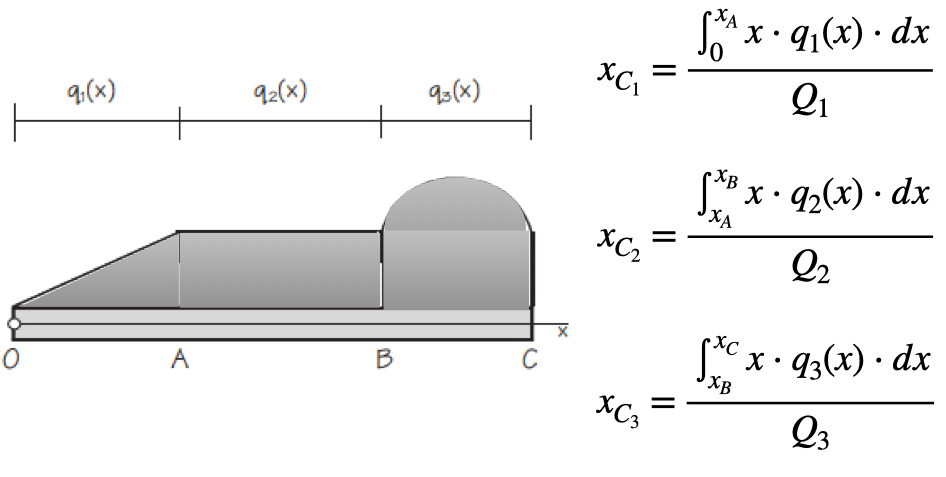
Figure shows a statically determinate beam that is supporting a general distributed load. The intensities qi(x) of a distributed load may be expressed as force per unit of length of beam. The intensity may be constant or variable, continuous or discontinuous. The intensity of the loading in Figure is constant from A to B and variable from O to A and from B to C. Although the intensity itself is not discontinuous at A and B, the rate of change of intensity dq/dx is discontinuous.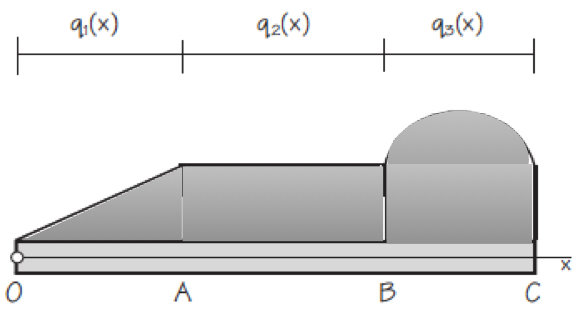 Any distributed load can be replaced by a concentrated load with a magnitude equal to the area under the load curve and a line of action passing through the centroid of the area. Therefore, we need to determine the equivalent force of the distributed force, i. e. the resultant, and the centre of gravity where it will be applied. Once the distributed loads have been reduced to their equivalent concentrated loads, the external reactions acting on the beam may be found by a straightforward static analysis as developed in Chapter 6 (equilibrium).
Any distributed load can be replaced by a concentrated load with a magnitude equal to the area under the load curve and a line of action passing through the centroid of the area. Therefore, we need to determine the equivalent force of the distributed force, i. e. the resultant, and the centre of gravity where it will be applied. Once the distributed loads have been reduced to their equivalent concentrated loads, the external reactions acting on the beam may be found by a straightforward static analysis as developed in Chapter 6 (equilibrium).
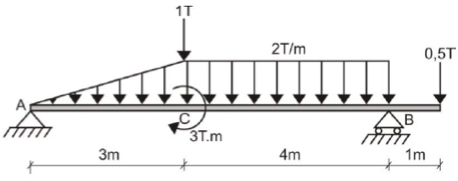
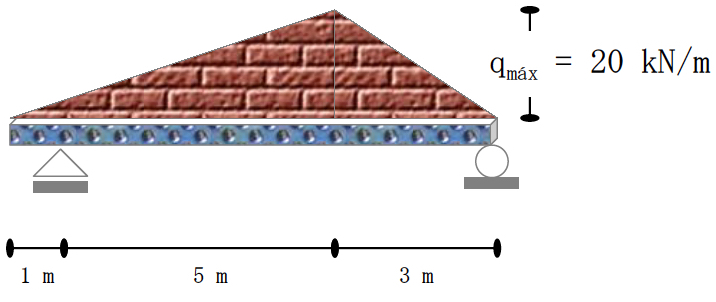
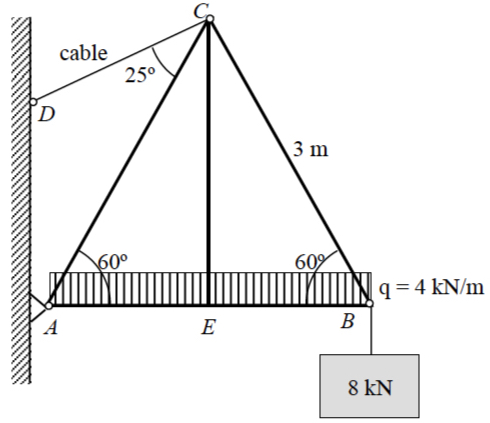
 EXERCISE 2: Draw the shear-force and bending-moment diagrams for the loaded beam and determine the maximum moment M and its location x from the left end.
EXERCISE 2: Draw the shear-force and bending-moment diagrams for the loaded beam and determine the maximum moment M and its location x from the left end.