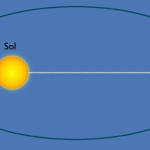
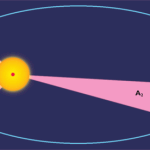
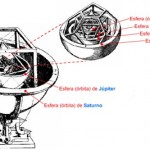
Galileo creía que era posible demostrar que el Sistema Heliocéntrico era una conclusión necesaria y evidente de los datos que se obtuvieron en esos momentos. Gracias a su telescopio, pudo ver un modelo del Sistema Solar en júpiter y sus satélites y pudo medir la gran variación anual de los diámetros aparentes de Venus y Marte.
Sus observaciones de las fases de Venus hicieron posible confirmar la predicción del Sistema copernicano de que los planetas mostrarían sus fases completas, como la Luna, cuando eran observados desde la Tierra.
Tal y como él dijo: “muchas otras observaciones sensibles que no pueden de ninguna manera ser reconciliadas con el sistema ptolemaico, sino que son los argumentos más fuertes en favor del sistema copernicano“.
Si la teoría copernicana fue prohibida y declarada contraria a la fe católica sin prohibir la Astronomía como un todo, el que Galileo continuara con su defensa provocó inevitablemente un gran escándalo.