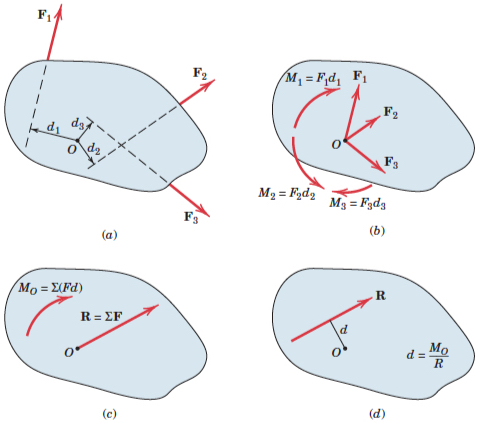
Any system of forces may be replaced by a resultant force R and a resultant moment (couple of a force) M at any point of the space. We call this couple vectors (R, M) as system “torsor”. Figure (from Meriam & Kraige 7th edition) shows a system of forces acting on a rigid body.
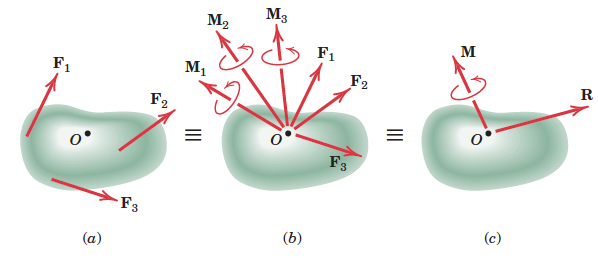 The point O selected as the point of concurrency for the forces is arbitrary, and the magnitude and direction of M depend on the particular point O selected. The magnitude and direction of R, however, are invariant, i.e. are the same no matter which point is selected.
The point O selected as the point of concurrency for the forces is arbitrary, and the magnitude and direction of M depend on the particular point O selected. The magnitude and direction of R, however, are invariant, i.e. are the same no matter which point is selected.
If a system of forces acting on a body are such that the resultant force and resultant moment at point O are mutually perpendicular, the whole system can be replaced by a single force acting along a new line of action such that it causes the same moment with respect to O. We now examine the resultants for several special system of forces:
- Concurrent forces: because there are no moments about the point of concurrency, system “torsor” at this point is only the resultant force R.
- Parallel forces: not all in the same plane, the magnitude of the parallel resultant force R is simply the magnitude of the algebraic sum of the given forces. The position of its line of action is obtained from the principle of moments by requiring that r × R = MO. Here r is a position vector extending from the force–couple reference point O to the final line of action of R, and MO is the sum of the moments of the individual forces about O.
- Coplanar forces: it may be reduced to only the resultant force R provided the line of action of R is passing through the centre of the system of forces, as shows Figure (rom Meriam & Kraige 7th edition):
Let’s consider a 2D situation. A rigid body under the action of forces (which are necessarily coplanar) can only be in equilibrium if the system of forces seen in the free-body diagram can be reduced to three concurrent forces that meet at a point that is inside the body.
Three concurrent forces at point C which is inside the rigid body: EQUILIBRIUM (upper figure).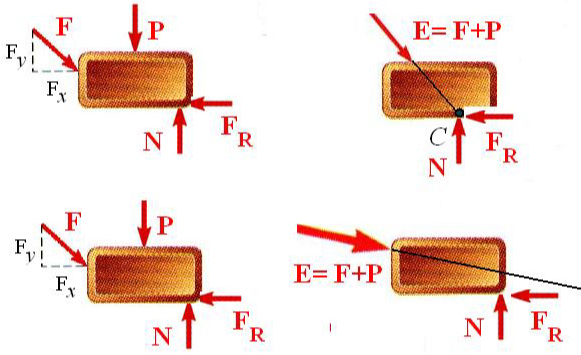 Three non-concurrent forces inside the rigid body:
Three non-concurrent forces inside the rigid body: 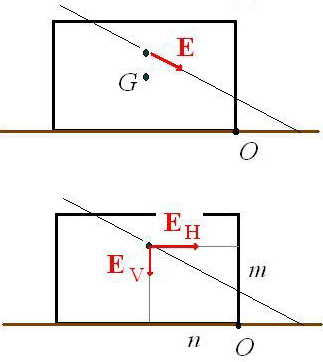 THERE IS NO EQUILIBRIUM (bottom figure). Therefore, if a body is not in equilibrium, we can check if it is prone to overturning or stable against toppling. For this, we calculate the resultant of all external forces and draw it at the point where its line of action cuts the line of action of the weight. Assume the rigid body can rotate about point O, we call rollover moment the expression:
THERE IS NO EQUILIBRIUM (bottom figure). Therefore, if a body is not in equilibrium, we can check if it is prone to overturning or stable against toppling. For this, we calculate the resultant of all external forces and draw it at the point where its line of action cuts the line of action of the weight. Assume the rigid body can rotate about point O, we call rollover moment the expression: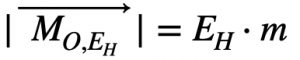
and stabilising moment the expression: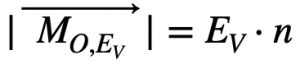
If the rollover moment is larger than the stabilising moment, the rigid body will turn over.