Problema propuesto en la prueba PSAT de la Universidad de Princeton, en 1981
Se dirige a una edad de: 16/17

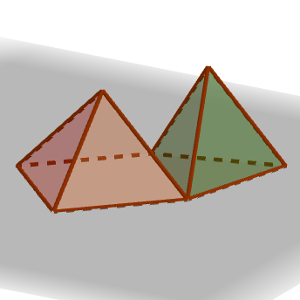
Disponemos de dos pirámides, cuyas caras laterales son todas triángulos equiláteros. Una es de base cuadrada y la otra, de base triangular.
¿Cuántas caras tiene el sólido que formamos si las unimos por una de las caras laterales?

Este problema tiene detrás una curiosa historia, de la que hablaremos cuando pongamos la solución.

Parece un problema muy sencillo, pero es engañosamente fácil.

La pirámide de base cuadrada tiene cinco caras: la base, que es un cuadrado, y las cuatro caras laterales (triángulos equiláteros).

La pirámide de base triangular (tetraedro regular) tiene cuatro caras en total (todas triángulos equiláteros).

Podemos pensar que si unimos ambas figuras por una cara, las caras que hemos usado para unirlas ya no podemos contarlas, de forma que tendríamos un total de 5 + 4 – 2 = 7 caras.

Sin embargo, en este caso no es así.

Antes de acabar la cuenta, es preciso comprobar si alguna de las caras que rodea a la cara de unión está en el mismo plano que las caras que rodean a las de la otra figura, y esto no es ni mucho menos evidente.

Es decir, que si dos caras de las que rodean a la zona de unión están en el mismo plano, en realidad ambas caras pasan a ser una única cara. Y en la figura que nos ocupa, eso sucede con dos pares de caras, que originalmente eran triángulos, y pasan a ser cuadriláteros por estar en el mismo plano. La figura que logramos es algo extraña, ya que tiene entonces 5 caras (7 – 2), de las cuales tendremos un cuadrado, dos cuadriláteros que son rombos de ángulo menor 60 grados, y dos triángulos equiláteros.

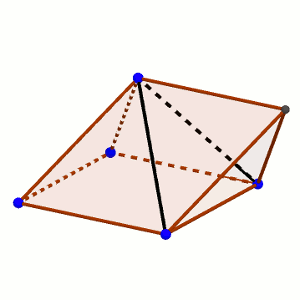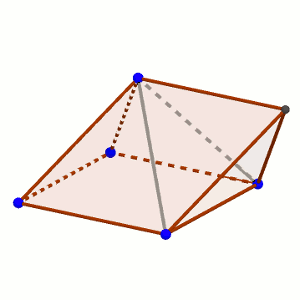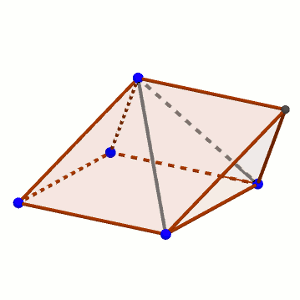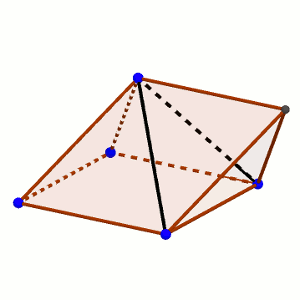
Puesto que en la competición se pedía sólo la respuesta y no el razonamiento, podías decir 5, o decir 7, y al parecer en un principio el jurado consideró que la respuesta válida era 7. Sin embargo, la reclamación de un participante tuvo que ser tenida en consideración, y cambiaron la respuesta válida a 5, que era la correcta.

La pregunta formaba parte de la prueba preliminar del test de aptitud escolar (PSAT) relacionado con la Universidad de Princeton, que decide la inclusión de los participantes en un programa de becas, y la reclamación del concursante obligó a cambiar la puntuación de los 250000 participantes, puesto que la puntuación de cada apartado depende de su dificultad, es decir, de cuánta gente la haya respondido correctamente.

El estudiante Daniel Lowen pensó que se trataba de un error en la calificación, no de que la pregunta estuviese incorrectamente valorada por el jurado.

Y dejamos para el final la parte más difícil. ¿Cómo podemos estar completamente seguros de que están en el mismo plano, y no se trata sólo de una apariencia, de un efecto óptico?

Hay dos formas. Por un lado, podemos tratar de estudiar los ángulos que forman las dos caras, utilizando segmentos perpendiculares a las aristas.

Por otro lado, podemos utilizar vectores, construyendo el vector perpendicular a ambas caras, para estar seguro de que son paralelos. Pero para hacer eso se utilizan técnicas que se estudian en segundo de bachillerato, como es el producto vectorial para levantar perpendiculares.

Con el primero de los métodos, hay que levantar perpendiculares a una arista por la cara de contacto y la otra. Dada la simetría del dibujo, optaremos por levantarlas en el punto central, por lo que medirán lo que miden las alturas de un triángulo equilátero. Al unirlas por el otro extremo, la cosa cambia si se hace en una de las figuras o en la otra. En el tetraedro, se cierran con un segmento que mide lo que el lado, mientras que la pirámide cuadrada se cierra con una diagonal del cuadrado de la base.

Si nos fijamos en las medidas, suponiendo que tomamos de unidad la longitud de cualquiera de las aristas, en el caso del tetraedro, las dos alturas miden raíz de 3 partido por dos, mientras que el otro segmento mide uno. En la pirámide cuadrada, las dos alturas miden raíz de 3 partido por dos, mientras que el otro segmento mide raíz de 2, es mucho más largo.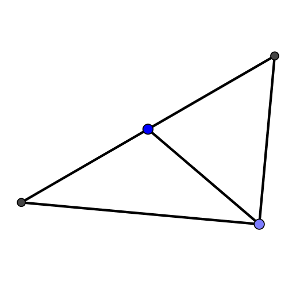

Ahora, para comprobar que realmente esos dos ángulos suman 180 grados, vamos a imaginar que unimos esos dos triángulos isósceles por uno de los lados comunes (como realmente pasa en la figura tridimensional). Observa que las perpendiculares sobre el lado desigual miden exactamente la mitad que el otro lado desigual. Efectivamente, en uno de ellos, aplicando Pitágoras, tenemos que 3/4 – 1/2 = 1/4, por lo que la altura mide 1/2. En el otro, de nuevo con Pitágoras, 3/4 – 1/4 = 1/2, con lo que la altura mide la mitad de la raíz de 2.

Eso quiere decir que las dos alturas forman un ángulo recto, es decir, que en efecto los dos ángulos de las caras suman 180 grados, es decir, que la figura tiene sólo cinco caras.

Queremos dar las gracias a nuestro amigo el profesor Juan Manuel Conde Calero, quien nos relató la anécdota y nos dio a conocer este curioso problema.