Problema 6 del concurso Marató de problemes 2024
Se dirige a una edad de: 14-15 años

En un triángulo ABC, trazamos dos paralelas a la base AB por dos puntos M y N del lado AC, que llegan, respectivamente a los puntos P y R del lado AB.

En el primer caso, cuando la trazamos por M, la proporción AM/MC es p y medimos el área del trapecio MABP.

En el segundo caso, medimos el área del triángulo NRC, y resulta ser la misma que la del anterior trapecio. ¿Qué proporción AN/NC hay?

Solución: Aquí.

Problema 1 del nivel B de la Olimpiada Autonómica de la Comunidad Valenciana
Se dirige a una edad de: 14 -15 años

Se tienen 4 perlas idénticas de color blanco, y otras 4 perlas de color negro.

Si giras un brazalete, o haces una simetría (es decir, le das la vuelta) se considera el mismo brazalete. Por ejemplo, los tres brazaletes de la imagen se consideran iguales.

Razona cuántos brazaletes diferentes se pueden hacer usando las ocho perlas.

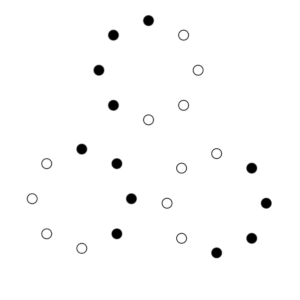
Solución: Aquí.

La teoría de los objetos fractales constituye el contexto matemático idóneo para el estudio y representación de ciertos fenómenos naturales asociados a formas o estructuras sumamente irregulares. Un mayor número de aplicaciones surge cuando se maneja el concepto teórico de multifractalidad, cuya teoría asociada puede ser considerada como una generalización del estudio base de los objetos fractales.

El uso cotidiano de la palabra fractal suele estar vinculado a un objeto geométrico cuya estructura básica, fragmentada o irregular, se repite a diferentes escalas (algo así como objetos geométricos sobre los que se puede divisar que sus partes tienen misma o similar estructura que el todo). Aunque varias de las ideas involucradas en lo que hoy conocemos como teoría de los objetos fractales eran conocidas mucho antes, el término fractal (procedente del vocablo latino fractus que se traduce como quebrado o fragmentado) fue propuesto en 1975 por el matemático Benoît Mandelbrot (1924-2010), considerado el principal responsable del auge de la geometría fractal.

Benoît Mandelbrot (1924-2010)

En contraposición con la geometría clásica de Euclides (la que se estudia desde las primeras etapas escolares y está basada en puntos, rectas y planos que pueden describirse y manipularse mediante expresiones matemáticas sencillas), la geometría fractal proporciona un marco general para el estudio formal de este tipo de objetos geométricos irregulares cuya construcción y desarrollo teórico nos sumerge en el mundo matemático de los procesos infinitos. De hecho, las ampliaciones sucesivas en fragmentos concretos de estos objetos geométricos tipo fractal no nos conducen necesariamente a visualizar únicamente un trazo rectilíneo. Más bien, cada zoom o ampliación realizada nos puede proporcionar una gráfica similar a la global (algo así como copias más pequeñas de la propia figura inicial), lo que se relaciona directamente con la propiedad llamada de autosemejanza que conduce ciertamente a una colección particular de fractales (los fractales autosemejantes).

Esta propiedad de autosemejanza, concebida como la invariabilidad en la forma o estructura del objeto independientemente de la escala empleada (y que se puede definir matemáticamente de una forma exquisita a través de transformaciones de semejanza contractivas), la podemos percibir en la naturaleza de forma intuitiva o aproximada en el caso de que, por ejemplo, nos detengamos a observar con atención la estructura de algunas clases de plantas o árboles (por ejemplo, en una cabeza de coliflor y en algunas clases de helechos en los que cualquier hoja parece una réplica de la figura completa) o el contorno de algunas nubes (lo que en la lejanía se percibe como una única nube, visto de más cerca pueden aparecer fragmentos más pequeños que se repiten a diferentes escalas). En varias ocasiones la literatura también se refiere a este tipo de ejemplos como fractales naturales en el sentido de que la propiedad de autosemejanza serviría únicamente para dar una idea aproximada de la estructura de estos objetos reales o fenómenos naturales.

Estructura fractal del Romanescu y el adianto negro (helecho común en zonas lluviosas).

Un ejemplo representativo de fractal matemático se debe al científico polaco Wacław Franciszek Sierpiński (1882-1969) que ideó su construcción en 1915. Mostraremos a continuación cómo diseñar este objeto geométrico, muy atractivo a nivel visual. Dado un triángulo sólido cualquiera, unamos primeramente los puntos medios de cada uno de sus tres lados, lo que generará cuatro triángulos interiores al triángulo inicial (todos del mismo tamaño). A continuación, eliminemos el triángulo central (su interior) y reproduzcamos el mismo proceso con cada uno de los otros tres triángulos resultantes. Si repetimos este procedimiento geométrico de forma indefinida, obtendremos una secuencia de objetos o conjuntos que, desde un punto de visto topológico, son cerrados, acotados y no vacíos. Así, los puntos que permanecen al límite, es decir, la intersección (infinita) de los conjuntos generados por todas las iteraciones, son los que forman el llamado triángulo de Sierpinski.

Aproximación al triángulo de Sierpinski

A partir de un triángulo en el plano (de dimensión usual o topológica igual a 2, ya que podemos calcular fácilmente su área), hemos visto que para generar el triángulo de Sierpinski se van extrayendo triangulitos cada vez más pequeños y finalmente, en el límite, se obtiene un objeto geométrico que es algo menos que una superficie. De hecho, no es muy complicado apreciar que el área de la figura resultante en cada iteración tiende a 0, pero el perímetro de la figura resultante o la suma de la longitud de los lados que forman las sucesivas figuras geométricas que se generan en cada etapa tiende a infinito. En general, esto hace que no sea descabellada la idea de asociar una dimensión no entera a un objeto fractal a caballo entre la línea y la superficie (para recoger eficazmente tanto su grado de irregularidad y fragmentación, como su eficacia para ocupar o llenar un espacio o conjunto, reflejando propiedades de escalado y autosemejanza). En el caso del triángulo de Sierpinski, la dimensión (de autosemejanza) asociada es de log 3/log 2.

Es importante notar que la forma de obtener ese valor no es casual. Si troceamos en partes iguales cada uno de los lados de la figura inicial, ciertamente su dimensión de autosemejanza se calcula como el valor d que satisface la igualdad s^d=N, donde N es el número de partes obtenidas y s es el número de divisiones en cada lado (equivalentemente, por las propiedades del logaritmo, obtenemos d=log N/log s o d=-log N/log r, donde r=1/s sería el factor de escala utilizado). Por ejemplo, si tomamos un cuadrado, que se puede contemplar como unión de cuatro cuadraditos iguales con longitud de lado la mitad del inicial (por tanto, 2 divisiones del lado), este valor d satisface 2^d=4, esto es, d=2, que es coherente con la dimensión usual o topológica del cuadrado. En el caso del triángulo de Sierpinski, tenemos que s=2 y N=3, lo que nos da justamente el valor d=log 3/log 2.

Son muchas las variantes y extensiones existentes del triángulo de Sierpinski. Por ejemplo, en el caso tridimensional (en el espacio) un proceso análogo de construcción se puede implementar a partir del uso de tetraedros (pirámides triangulares), lo que conduciría al llamado tetraedro de Sierpinski, o incluso con pirámides de base rectangular.

Más allá de este tipo de estructuras geométricas recursivas, y desde un punto de vista estrictamente matemático o formal, la existencia de fractales autosemejantes en el mundo real no es plausible. En efecto, tal como ocurre en los candidatos naturales mencionados con anterioridad, no se perciben copias reducidas del objeto inicial que sean totalmente exactas y, además, se observa únicamente un número finito de niveles de autosemejanza. Sin embargo, el análisis fractal también abarca la posibilidad de identificar en estas formas enmarañadas algún tipo de patrón fractal imperfecto o aproximado, y limitado por varios factores naturales. Un claro ejemplo de ello lo constituye el tratamiento de las imágenes digitales, ampliamente utilizadas para el diagnóstico médico.

El hecho de proporcionar un valor numérico que represente fielmente el tamaño y la forma irregular de alguno de estos elementos naturales no es en general una tarea fácil. Un parámetro que se utiliza habitualmente para identificar un patrón fractal es la llamada dimensión por recuento de cajas, que funciona a base de correlacionar las observaciones a diferentes escalas del mismo fragmento analizado, y que es compatible con el valor de la dimensión (fractal) obtenido con anterioridad.

En el contexto de las imágenes digitales (y en otros como el de la predicción de terremotos o  las turbulencias de fluidos), en los últimos tiempos se ha incrementado el uso de la multifractalidad, que contempla la posibilidad de analizar eficazmente la distribución de los píxeles identificativos del contorno estudiado, lo que permite estudiar más localmente su estructura interna y la variación existente en la morfología estudiada.

Para seguir adentrándose en esta teoría de los objetos fractales y multifractales, os remito ahora al artículo que escribí hace unas pocas semanas para Café y Teoremas, de El País, titulado “Geometría fractal para la detección eficaz de tumores” (y, por supuesto, a referencias matemáticas clásicas sobre geometría fractal como el libro de K. Falconer titulado Fractal Geometry, o sobre multifractalidad al libro de D. Harte titulado Multifractals: Theory and applications).

https://elpais.com/ciencia/cafe-y-teoremas/2022-03-01/geometria-fractal-para-la-deteccion-eficaz-de-tumores.html

Esta entrada también está inspirada en el trabajo de divulgación realizado en torno a las siguientes publicaciones:

(Libro) Sepulcre, J.M.: “La prevenzione dei tumori e la geometria frattale“, Vol. 34 de: “La Matematica che trasforma il mondo”, Milán, RBA Italia, 2021. ISSN: 2724-1726.

(Artículo) Sepulcre, J.M.: Geometría fractal: la geometría de la naturaleza, SUMA. Revista sobre la enseñanza y el aprendizaje de las matemáticas, Dic. 2020, nº 95, pp. 17-25, 2020.

Escrito por Juan Matías Sepulcre

Este post forma parte del Carnaval de Matemáticas, que en su edición 13.2, está organizado por Gaussianos.

No cabe duda que los números complejos juegan un importante papel en muchas áreas de las matemáticas y física teórica. Pero, ¿qué son realmente los números complejos? ¿cómo surgieron?

Comencemos por el concepto de unidad imaginaria, denotada por i, que se define a través de la relación i^2=-1. A partir de i y de los números reales, los números imaginarios aparecen como multiplicaciones de la propia unidad imaginaria por un número real… esto nos recuerda a la definición de los números enteros negativos en los que los números naturales son multiplicados por -1.

En relación a ello, para el siguiente razonamiento intuitivo tomemos por convenio que los números positivos son los que miran al norte y los negativos los que miran al sur. Mientras que únicamente en la recta real nos podemos mover hacia el norte o hacia el sur (a través del -1), de forma más general la multiplicación por la unidad imaginaria i nos proporciona otras posibilidades. En efecto, si nos situamos mirando hacia el norte, la multiplicación por i nos repercute en un giro de derechas hacia el este (por ejemplo, del número positivo 1 pasamos a la unidad imaginaria i). Una nueva multiplicación por i nos lleva ahora hacia el sur, cuya unidad es -1. De esta manera, i∙i=i^2=-1, con lo que i viene también a hacer el papel de √(-1), proporcionando una definición plausible de la unidad imaginaria. Continuando con este proceso, si multiplicásemos de nuevo por i llegaríamos a la unidad del oeste, es decir, i^3=-i, y una nueva multiplicación por i nos devolvería al norte, i^4=1. En definitiva, con la introducción de la unidad imaginaria hemos pasado de la dicotomía sur-norte de la recta real al descubrimiento de los otros dos puntos cardinales este-oeste. Esto podría ser generalizado aún más estableciendo otras direcciones en nuestra particular brújula.

El caso es que a través de los números reales e imaginarios podemos resolver cualquier ecuación puramente cuadrática, del tipo x^2=a, con a un número real. Ahora, si pensamos en el hecho que un número complejo se define como la suma de un número real y un número imaginario, el teorema fundamental del álgebra nos lleva al potente resultado consistente en afirmar que cualquier ecuación algebraica de grado n, con coeficientes complejos, presenta n soluciones complejas (teniendo en cuenta las multiplicidades). En particular, para una ecuación cuadrática, ax^2+bx+c=0, con coeficientes reales o complejos, siempre existen dos soluciones, no necesariamente distintas, que vienen dadas por las conocidas expresiones x=(-b+√(b^2-4·a·c))/(2·a) y x=(-b-√(b^2-4·a·c))/(2·a).

Para seguir adentrándose en este bello mundo, os remito ahora al artículo que escribí hace unas pocas semanas para el ABCdario de las matemáticas titulado “El bello mundo de los números imposibles”:

https://www.abc.es/ciencia/abci-bello-mundo-numeros-imposibles-201905060149_noticia.html

Esta entrada también está inspirada en el trabajo de divulgación realizado en torno al siguiente libro:

Sepulcre, J.M.: Weierstrass. La gestación del análisis moderno. ISBN: 978-84-473-8775-5, 156 páginas, Editorial RBA. Colección: Genios Matemáticos, 2017.

Escrito por Juan Matías Sepulcre

Este post forma parte del Carnaval de Matemáticas, que en esta octogésima tercera edición, también denominada X.3, está organizado por @Pedrodanielpg a través de su blog A todo Gauss. Finalmente esta entrada fue la ganadora de esta edición.

(more…)

Problema 2 de la Olitele 2018
Se dirige a una edad de: 16-17 años

En este ejercicio, [x] representa la parte entera del número x, y {x}, su parte decimal.

¿Cuánto suman las soluciones de la ecuación 10[x] + 20{x} = K?

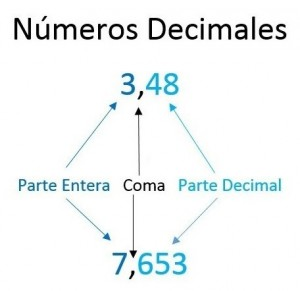
Solución: Aquí.

Si te declaras culpable de derivadas e integrales, curvas y superficies, variables aleatorias y funciones de densidad, anillos, cuerpos y conmutatividades varias…

¡Customiza tu foto en Powerpoint con unas rejas sobre un fondo matemático!

En 1747 Bach compuso la Ofrenda Musical BWV 1079 (Das Musikalische Opfer). Esta obra tiene su origen en un encuentro entre el compositor alemán y el rey Federico II de Prusia, en el cual Bach fue retado a improvisar un tema que sería la base del resto de piezas. La colección, que fue dedicada a este rey, se compone de cánones, fugas y otras piezas de carácter instrumental.

Pero el pensamiento matemático de Bach fue mucho más allá…

En uno de los cánones, titulado el Canon del Cangrejo y compuesto por procedimiento de inversión, el acompañamiento es una repetición exacta de la voz principal, pero en sentido inverso, pudiendo interpretarse tanto hacia delante como hacia atrás, así como simultáneamente.

Por tanto, si aislamos estas dos secciones y unimos de manera volteada el comienzo con el final, acaba resultando un ejemplo de la banda de Moebius (que sería descrita por August Moebius en 1858). El artista gráfico Jos Leys lo ha demostrado de una manera muy atractiva en este vídeo:

En el siguiente documento Plantilla_Moebius-Bach-1.pdf se puede descargar la plantilla para crear manualmente una banda de Moebius con el canon.

El presente post ha sido redactado por Laura Mondéjar (Twitter: @laurmondejar), pianista y profesora de la Fundación San Pablo Andalucía CEU.

Los partidos de la vigésimo primera edición del mundial de fútbol masculino de Rusia siguen registrando audiencias espectaculares. Como en ediciones anteriores, y en este caso hasta el 15 de julio que se celebrará la gran final, el Mundial suscita, entre otros aspectos, un sinfín de apuestas estrambóticas, polémicas arbitrales, pasiones nacionales, el show de Maradona, críticas a jugadores, entrenadores y presidentes de federaciones, divertidos memes y titulares llamativos como el de “Alemania no supera la maldición del campeón en la fase de grupos”, refiriéndose a la eliminación de ayer de Alemania en la primera fase del torneo.

Ciertamente, bajo el formato actual, Francia, Italia y España también cayeron en la primera ronda (en 2002, 2010 y 2014, respectivamente) cuando afrontaron un nuevo mundial para defender su corona, pero también es cierto que Brasil sí que superó la primera fase en 2006 habiendo ganado la edición previa. Encontrarnos esta excepción de Brasil en los últimos cinco mundiales (únicamente son los últimos cinco mundiales en los que se ha utilizado el formato actual) podría llevar a cuestionarnos el uso de la palabra maldición, que en cualquier caso queda muy llamativo en un titular de prensa.

El caso es que el hecho de que el campeón de la edición anterior tenga tantas dificultades para superar la primera fase (cuando a priori es uno de los grandes candidatos a superarla sin grandes dificultades), unido a que tengamos una excepción en la supuesta maldición del campeón, me ha llevado a pensar en el peligro de sacar conclusiones rápidamente y, en particular, dada mi profesión, a recordar algunos casos especialmente significativos que llevaron a no poder generalizar alguna propiedad matemática que “parecía” funcionar indefinidamente (esto es, para una cantidad infinita de valores enteros)… y es que la inducción se utiliza muy a menudo en matemáticas, pero se hace necesario emplearla correctamente. Veamos algunos ejemplos de ello.

• El gran matemático G. W. Leibniz probó en el siglo XVII que:

> n^3-n es divisible por 3 para todo n natural;
> n^5-n es divisible por 5 para todo n natural
> n^7-n es divisible por 7 para todo n natural

Como en el caso de la “maldición” del campeón en la fase de grupos (recordemos, Francia, Italia y España), disponemos aquí también de tres casos que podrían llevarnos a pensar en la aparente propiedad:

“Si k es impar, n^k-n es divisible por k para todo n natural.”

Sin embargo, Leibniz probó posteriormente que:

2^9-2=510 no es divisible por 9,

lo que desmonta la afirmación genérica.

• Un ejemplo, más conocido que el anterior, hace referencia a los números de la forma 2^{2^n}+1, llamados números de Fermat, que sabemos que son números primos para los primeros cinco casos n=0,1,2,3,4 (por tanto, más casos que los que proporcionan la “maldición” del campeón en la fase de grupos). En efecto:

> Si n=0, obtenemos 2^{2^0}+1=3 que es primo;
> Si n=1, obtenemos 2^{2^1}+1=5 que es primo;
> Si n=2, obtenemos 2^{2^2}+1=17 que es primo;
> Si n=3, obtenemos 2^{2^3}+1=257 que es primo;
> Si n=4, obtenemos 2^{2^4}+1=65537 que es primo;

Sin embargo, L. Euler demostró en el siglo XVIII que:

2^{2^5}+1 = 4294967297 = 641 · 6700417 no es primo.

Por cierto, si no os gusta el fútbol y estáis estos días ociosos, podéis probar a responder de forma justificada a las siguientes preguntas en relación a este ejemplo: ¿Hay infinitos números de Fermat que sean primos? ¿Sólo hay cinco números primos de Fermat (3, 5, 17, 257 y 65537)? En este caso no os puedo proporcionar la respuesta ya que se trata de dos conocidos problemas aún sin resolver 🙂

• La propiedad que os muestro en la imagen siguiente (cierta para n<105 pero que falla en el caso n=105) se terminó de clarificar cuando en 1941 se publicó la solución proporcionada por V. K. Ivanov.

• Otro ejemplo en el que el patrón se rompe es el que os muestro en la siguiente figura. En concreto, la pauta se rompe en la octava integral impropia cuyo resultado es un valor cercano a π/2, pero no es π/2. Esto muestra la necesidad de ser prudentes con nuestras afirmaciones:

• En un artículo de 2006 por D. H. Bailey, J M. Borwein, V. Kapoor y E. W. Weisstein, y gracias a la ayuda del utilizado programa Mathematica (con la opción especial de calcular 100 dígitos de la parte decimal de una constante requerida), se hacía alusión a que el valor de la expresión que aparece en la siguiente imagen difiere de π/8 únicamente a partir del decimal número 42. Casi nada al aparato…

• Decimos que un número entero es un “cuadrado perfecto” cuando es el cuadrado de algún otro (esto es, un número cuya raíz cuadrada es un número natural). Como de nuevo muestra este ejemplo, no basta comprobar la veracidad de una propiedad para unos cuantos valores de n. En este caso, el ordenador nos indica que 991n^2 + 1 no es un cuadrado perfecto para n=1,2,3,…, 12055735790331359447442538766, pero ¡¡¡ sí lo es para 12055735790331359447442538767 !!!

• En 1772 Leonhard Euler se dio cuenta que el polinomio cuadrático P(n)=n^2+n+41 proporciona números primos para n=0,1,…,39. Sin embargo, P(40)=1681=41·41. (De hecho, P(n)=n·(n+1)+41 lo que significa que si n es múltiplo de 41 o n+1 es múltiplo de 41 entonces P(n) ya no es primo).

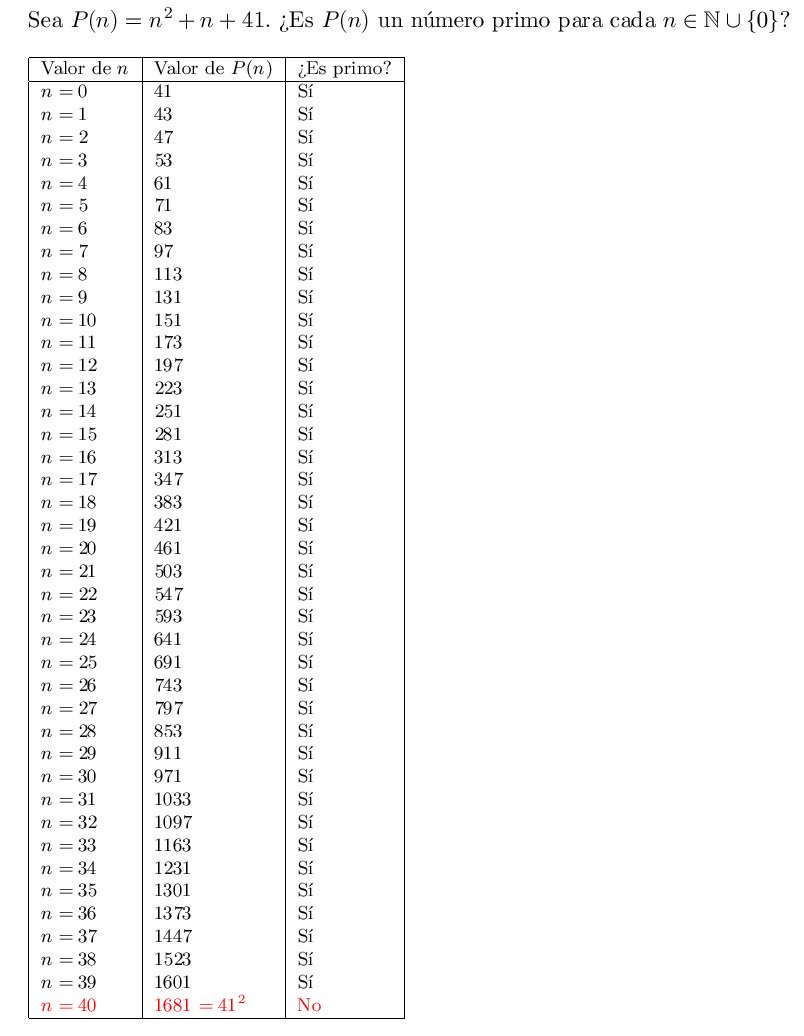
De hecho, P(n)=n^2+n+p genera números primos consecutivos únicamente para seis valores primos de p (los afortunados de Euler), y entre ellos encontramos a p=41.

• Os muestro otro interesante ejemplo a través del llamado problema de la región perdida. Señalemos n puntos sobre una circunferencia de tal modo que al trazar todas las cuerdas posibles que los unen de dos en dos no haya tres cuerdas concurrentes. ¿En cuántas regiones queda dividido el círculo por estas cuerdas? Podemos comprobar que para n=2, 3, 4 y 5 puntos resultan 2 = 2^1 , 4 = 2^2 , 8 = 2^3 y 16 = 2^4 regiones, respectivamente. Sin embargo, para n=6 sólo resultan 31 regiones y no 2^5=32, de ahí el nombre del problema. Entre partido y partido del mundial, retamos al lector a encontrar la explicación de este hecho (si estáis interesados en la resolución también me podéis escribir y os la proporciono).

En definitiva, espero haber hecho hincapié en el peligro de sacar conclusiones rápidamente. Por cierto, ¿ocurrirá lo mismo en la próxima edición del mundial de fútbol? ¿entrará de nuevo en juego la “maldición” y tendremos eliminación del campeón en Catar2022? Desde luego, lo que ya sabemos a estas alturas es que no podremos dar por hecho que el que tenga todas las papeletas para franquear la siguiente fase vaya realmente a superarla.

Escrito por Juan Matías Sepulcre

Este post forma parte del Carnaval de Matemáticas, que en esta septuagésima octava edición, también denominada 9.2, está organizado por @Pedrodanielpg a través de su blog A todo Gauss. Finalmente el post quedó en segunda posición de esta edición con 41 puntos recibidos.

España es un país de bares. Lo sé, esto no va a sorprenderle. En junio de 2017, el número de bares en España ascendía a 101397, es decir, 2.8 bares o cafeterías por cada 1000 habitantes. Quizás le sorprenda más saber que las capitales con más bares por habitante no son ni Granada, ni Sevilla, ni siquiera Madrid, sino León, Salamanca y Zamora (ver, por ejemplo, este enlace).

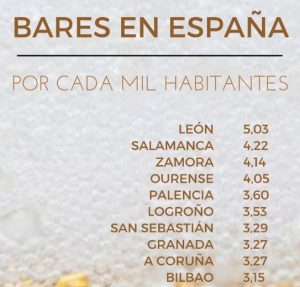
Por otra parte, España ha pasado a los octavos de final del mundial de Rusia gracias al VAR (video assistant referee, por si no lo sabía) y, lo sé, esto tampoco le va a sorprender. En este sentido, el VAR consiste en una serie de cámaras que deben servir para reducir la incertidumbre en el arbitraje de un partido de fútbol).

Sin embargo, el VaR, así con uve, y en mayúsculas y minúsculas, siglas de Value at Risk (en inglés) o Valor en Riesgo (en español), es una noción matemática de suma importancia, por ejemplo, en finanzas que ya existía mucho antes del mundial de Rusia y que persigue, de alguna manera, el control de la incertidumbre, expresada como un riesgo.

El término riesgo tiene muchas acepciones dependiendo de la persona y del contexto en el que nos refiramos a él. El riesgo de no estudiar para un examen es suspenderlo, el riesgo de hacer una escape room es no salir de ella, el riesgo de hacer una entrada dentro del área es que te piten penalti y el riesgo de comprar una papeleta de lotería es perder el dinero que nos costó. En general, y hablando muy coloquialmente, podríamos coincidir en que el riesgo es la posibilidad (o no) de experimentar ciertos eventos de interés y las consecuencias derivadas de ellos (que no tienen por qué ser negativas, oiga).

Fijemos una situación desde un punto de vista bien sencillo: piense el lector que dispone de un activo financiero A que puede reportarle beneficios (o pérdidas, que es lo que más “debería” interesarnos). Si yo le digo que el VaR (value at risk, valor en riesgo) de dicha inversión A (al 95%, por defecto) es de 100 euros, debe entender que 100 euros es la máxima pérdida que usted sufrirá el 95% de las ocasiones durante cierto periodo de tiempo. También podríamos pensar que sólo el 5% de las ocasiones perderemos más de 100 euros.

Suponga ahora que yo, como inversor prestigiosísimo, le propongo una inversión B cuyo VaR (de nuevo, al 95%) es de 50 euros o, lo que es lo mismo, si usted me lo compra el 95% de las ocasiones sufrirá una pérdida menor de 50 euros ¿qué activo financiero preferiría: A ó B? No es aventurado pensar que la mayoría de ustedes preferirían B. Además, si se lo digo yo, que soy gran conocedor de las finanzas…

Y la respuesta es que sí: es cierto que, a priori, podríamos estar de acuerdo, que todos dispondríamos de la inversión B en nuestra “cartera” y que todos esperaríamos obtener muchos beneficios o, al menos, perder menos que aquéllos propietarios de la inversión A.

Si bien es cierto que inversores de todo el mundo llevan años preocupados por medir el posible riesgo existente a la hora de adquirir una cartera, no fue hasta finales de 1980 cuando surgió el concepto de VaR que acabamos de comentar. En 1987, y después de una fuerte crisis financiera, Dennis Weatherstone (presidente de la compañía financiera estadounidense JP Morgan & Co.) tomó la decisión de solicitar un informe breve y diario donde se plasmase el riesgo de pérdida en cartera durante las siguientes 24 horas y este fue el origen del uso del VaR como medida de riesgo. Esta medida cobró tal importancia a lo largo de los años que terminó por convertirse en la herramienta más utilizada a nivel mundial para medir el posible riesgo a la hora de invertir en una determinada cartera. De hecho, el Comité de Supervisión Bancaria de Basilea, es decir, la organización mundial que reúne a las autoridades de supervisión bancaria a fin de fortalecer la solidez de los sistemas financieros y reducir el riesgo, y que se reúne periódicamente, estableció en origen un VaR al 95% como medida de riesgo preferente y, en 1995, aumentó el nivel al 99%, es decir, querían controlar no el 95% de las ocasiones, sino el 99%.

Desde el punto de vista matemático, si X es una variable aleatoria que expresa los beneficios o pérdidas de una inversión el VaR no es más que la función cuantil evaluada en cierta probabilidad p=0.95 ó p=0.99. No se agobie, si usted es madre o padre, seguro que ha usado la función cuantil anteriormente. Si le dicen que su hijo, que tiene 5 semanas y pesa 4.8 kg, está en el percentil 72.6, seguramente se quedará tranquilo, porque esto querrá decir que el peso de su bebé es mayor que el peso de aproximadamente el 73% de los niños de su edad (ver la siguiente figura, http://www.percentilesinfantiles.es/). Evidentemente, esto ha sido calculado a partir de los pesos registrados de miles y miles de bebés de su edad y es una buena señal del crecimiento. Los 99 posibles percentiles no son más que algunos (pocos) casos particulares de los infinitos cuantiles.

Hasta aquí todo, más o menos, bien, pero volvamos a nuestra inversión porque no es oro todo lo que reluce. Decíamos que si el VaR al 95% es igual a 100 euros, “esperaremos” no superar los 100 euros de pérdida en el 95% de las ocasiones, pero no se deje engañar: ¿qué ocurre el 5% restante? ¿Y si, por cosas del destino, una de esas veces ocurre que perdemos un millón de euros? Piénselo, algunos caminos son inexcrutables y hablar de probabilidades es simplemente eso: hablar de probabilidades.

Pero… realmente ¿puede ocurrir que perdamos un millón de euros cuando sabemos lo que ocurre el 95% de las veces? Pues ¡vaya que sí! Y si no que se lo digan a los gurúes de Wall Street o a nuestros amigos de JP Morgan. ¿Recuerdan la crisis que comenzó en 2008? Si todo estaba controlado (y bien controlado) por nuestro querido VaR, ¿cómo fue posible aquel batacazo económico mundial del que 12 años después aún no nos hemos recuperado?

Sea como fuere, se perdió de vista que lo único que mide el VaR es una probabilidad. Más concretamente, en tal caso hay un 99% de probabilidades de “no perder”, pero nadie miró a ese 1% restante hasta que finalmente sucedió y las pérdidas se acumularon en miles de millones, dando como resultado un efecto dominó que, sumado a la ineficacia, ineficiencia e ignorancia de los políticos, ya sabemos lo que provocó.

Ante tal catástrofe, el Comité de Basilea publicó en 2010 una revisión de los criterios oficiales para el control del riesgo promoviendo un cambio hacia otra medida de riesgo que sí tiene en cuenta el peso de las mayores pérdidas. Pero ojo, no cometamos de nuevo el error de pensar que lo que tiene probabilidades bajas de suceder, no sucederá.

Así que estimado lector o lectora, no hay nada como el calor del amor en un bar y tampoco hay nada que un VAR en el último minuto no arregle, pero nada como un VaR bien controladito para poder ir ver a España ganar el mundial de Rusia con un buen gin tonic entre las manos.

Escrito por Julio Mulero

Este post forma parte del Carnaval de Matemáticas, que en esta septuagésima octava edición, también denominada 9.2, está organizado por @Pedrodanielpg a través de su blog A todo Gauss.