El término falacia matemática se emplea normalmente para designar un razonamiento erróneo pero con la apariencia de raciocinio correcto, es decir, persuasivo o engañoso. En particular, algunas falacias matemáticas han llegado a cautivar la atención del gran público por lograr “probar” (evidentemente de forma errónea), a través de unos pocos pasos, igualdades imposibles del tipo 0=1 o 1=2.

En esta entrada veremos algunos ejemplos significativos de falacias en las que el razonamiento erróneo se debe a una mala o inadecuada interpretación de alguno de los elementos o definiciones que entran en juego (lo que lleva implícito a su vez una falta de rigor matemático), y otras en los que el motivo es un procedimiento erróneo de cálculo.

• ¿0=1? Observemos con atención  
  En esta primera falacia matemática que os muestro en la imagen que viene a continuación, la expresión inicial en la que aparece el símbolo de la integral acompañado de la función 1/(x ln x) nos lleva aparentemente a “probar” que 0=1. Por tanto, el tópico principal de esta falacia es el cálculo de primitivas.

La clave está en el hecho de que estamos trabajando con el concepto de integral indefinida. Una inspección inicial nos puede llevar a pensar varios hechos:

-Por ejemplo, conviene inicialmente notar que se puede calcular una primitiva de forma inmediata, ya que la expresión del integrando (recordemos, 1/(x ln x)) responde a la forma f'(x)/f(x), con f(x)=ln x, pero eso no elimina la posibilidad de poder en principio utilizar integración por partes…

-Además, para que tenga sentido calcular primitivas de la función 1/(x lnx) se supone ya desde el principio que trabajamos en el dominio de dicha función, es decir, en el conjunto {x en R: x>0, x≠1}. Por ejemplo, podemos suponer que, sin pérdida de generalidad, se trabaja en un intervalo [a,b] incluido en (0,1) o incluido en (1,∞), y que se pretende calcular primitivas de dicha función en un intervalo de esa forma. Así que el motivo de llegar a una contradicción no pasa por la ausencia de las condiciones habituales que se han de verificar para, por ejemplo, poder aplicar la integración por partes, ya que en efecto las funciones elementales que entran en juego satisfacen en dichos intervalos las condiciones de integrabilidad, e incluso sus derivadas son también integrables.

Os muestro a continuación la explicación que escribí sobre la contradicción obtenida anteriormente (conviene también mencionar que en muchos textos y foros en los que se ha hecho alusión a falacias de este tipo se suelen omitir estas explicaciones).

• ¿2=1? Observemos con atención  
  En esta segunda falacia son las reglas básicas del álgebra y las operaciones con expresiones algebraicas las que entran en juego.

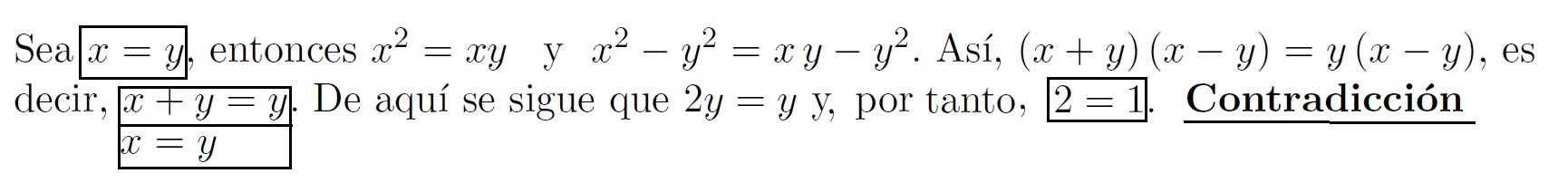
La razón de que lleguemos en este caso al absurdo 2=1 viene dada por el hecho de que x=y implica que x-y=0, por lo que al multiplicar y dividir por (x-y) estamos infringiendo las reglas básicas. En efecto, existen muchas falacias similares que se basan en multiplicar o dividir por un término que resulta ser idénticamente igual a 0.

• ¿0≥1? Observemos con atención  

Esta tercera falacia también involucra las reglas básicas propias de las desigualdades. Recordemos que si 1<2, entonces (-1)·1=-1>(-1)·2=-2, esto es, hemos de cambiar la desigualdad cuando multiplicamos por un número negativo.

• La cuarta y quinta falacia involucra a la unidad imaginaria i, símbolo introducido en la literatura por Leonhard Euler (recordemos que i^2=-1), y nos lleva a “demostrar” que 1=-1. Observemos con atención  

En ambos casos, la problemática está relacionada con el hecho de que no hay ninguna regla en el caso complejo que nos asegure que la raíz del producto (o del cociente) sea el producto de raíces (o el cociente de raíces). Si trabajáramos con números positivos, esta propiedad sí que sabemos que es cierta, pero en general no lo es.

Evidentemente estos casos son bastante llamativos debido a que se llega a igualdades imposibles que nos llevan de inmediato a la necesidad de comprobar cada uno de los pasos que se han utilizado en el razonamiento en cuestión. Esto muestra de nuevo la importancia del rigor y la especificación en el quehacer matemático.
Os animo a utilizar estas falacias como estrategia de motivación en vuestras tareas docentes.

Escrito por Juan Matías Sepulcre

PD: Esta entrada forma parte del Carnaval de Matemáticas que en esta octagésima edición, denominada 9.4 Regla y compás está organizada por Miguel Ángel Morales Medina a través de su blog Gaussianos. Finalmente el post quedó en segunda posición de esta edición con 11 puntos recibidos.