Home » Olimpiada Matemática Española
Category Archives: Olimpiada Matemática Española
Solución a “Una ecuación complicada”
Problema 7 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
Sea a > 1 un número real.
Encontrar todas las soluciones de la ecuación: raíz(a – raíz(a + x)) = x en función de a.
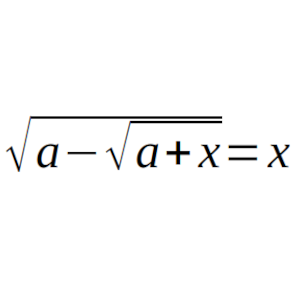
Solución:
(more…)
Una ecuación complicada
Problema 7 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
Sea a > 1 un número real.
Encontrar todas las soluciones de la ecuación: raíz(a – raíz(a + x)) = x en función de a.
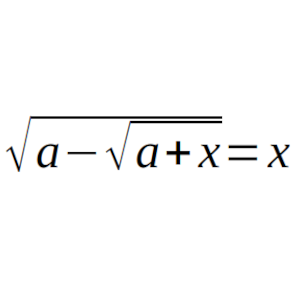
Solución: Aquí.
Solución a “Demasiados cuadrados”
Problema 6 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
Sean a, b, c tres números enteros, y sea p >= 5 un número primo.
Demostrar que, si an² + bn + c es el cuadrado de un número entero para 2p – 1 valores consecutivos de n, entonces b² – 4ac es un múltiplo de p.

Solución:
(more…)
Demasiados cuadrados
Problema 6 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
Sean a, b, c tres números enteros, y sea p >= 5 un número primo.
Demostrar que, si an² + bn + c es el cuadrado de un número entero para 2p – 1 valores consecutivos de n, entonces b² – 4ac es un múltiplo de p.

Solución: Aquí.
Solución a “La fiesta”
Problema 5 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
En una fiesta hay 100 personas. Cada par de personas son o bien amigos o bien enemigos (una y solo una de las dos cosas).
Se cumple la siguiente propiedad: si A y B son enemigos y B y C son enemigos, entonces A y C son amigos.
Demostrar que hay dos personas X e Y que cumplen simultáneamente estas condiciones:
X tiene el mismo número de enemigos que Y .
X e Y son amigos.

Solución:
(more…)
La fiesta
Problema 5 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
En una fiesta hay 100 personas. Cada par de personas son o bien amigos o bien enemigos (una y solo una de las dos cosas).
Se cumple la siguiente propiedad: si A y B son enemigos y B y C son enemigos, entonces A y C son amigos.
Demostrar que hay dos personas X e Y que cumplen simultáneamente estas condiciones:
X tiene el mismo número de enemigos que Y .
X e Y son amigos.

Solución. Aquí.
Solución a “Cometa sobre trapecio”
Problema 4 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
Sea ABCD un trapecio de bases AB y CD tal que AD = DC = CB = 5 y AB = 10.
Sea O el punto de intersección de las diagonales AC y BD.
La recta perpendicular a AC trazada por O corta a la prolongación del lado AD en E, y a la base AB en F.
Calcular el área del cuadrilátero AECF.
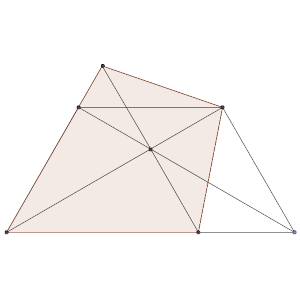
Solución:
(more…)
Cometa sobre trapecio
Problema 4 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
Sea ABCD un trapecio de bases AB y CD tal que AD = DC = CB = 5 y AB = 10.
Sea O el punto de intersección de las diagonales AC y BD.
La recta perpendicular a AC trazada por O corta a la prolongación del lado AD en E, y a la base AB en F.
Calcular el área del cuadrilátero AECF.

Solución: Aquí.
Solución a “Perpendicular en un cuadrilátero”
Problema 3 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
Sea ABCD un cuadrilátero.
Sean J e I los puntos medios de las diagonales AC y BD, respectivamente.
Sea G el punto de la recta BC tal que DG es perpendicular a BC y sea H el punto de la recta AD tal que CH es perpendicular a AD.
Las rectas DG y CH se cortan en el punto K.
Sea E el punto de la recta BC tal que AE es perpendicular a BC y sea F el punto de la recta AD tal que BF es perpendicular a AD.
Las rectas AE y BF se cortan en el punto L.
Probar que KL es perpendicular a JI.
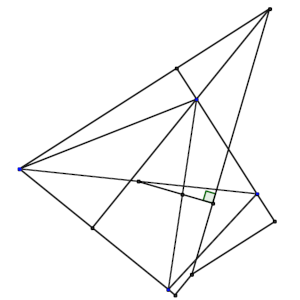
Solución:
(more…)
Perpendicular en un cuadrilátero
Problema 3 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
Sea ABCD un cuadrilátero.
Sean J e I los puntos medios de las diagonales AC y BD, respectivamente.
Sea G el punto de la recta BC tal que DG es perpendicular a BC y sea H el punto de la recta AD tal que CH es perpendicular a AD.
Las rectas DG y CH se cortan en el punto K.
Sea E el punto de la recta BC tal que AE es perpendicular a BC y sea F el punto de la recta AD tal que BF es perpendicular a AD.
Las rectas AE y BF se cortan en el punto L.
Probar que KL es perpendicular a JI.

Solución: Aquí.