Problema 4 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
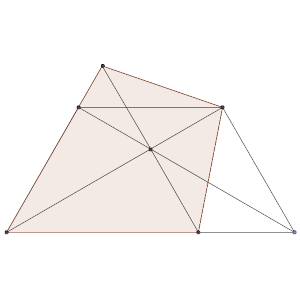
Sea ABCD un trapecio de bases AB y CD tal que AD = DC = CB = 5 y AB = 10.
Sea O el punto de intersección de las diagonales AC y BD.
La recta perpendicular a AC trazada por O corta a la prolongación del lado AD en E, y a la base AB en F.
Calcular el área del cuadrilátero AECF.
Solución:
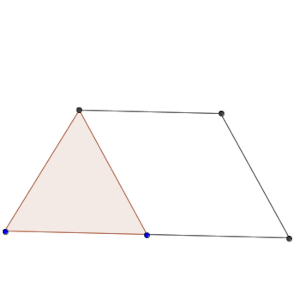
Construir la figura no es complicado, ya que si acercamos B y C 5 unidades a A y a D, respectivamente, veremos que se forma un triángulo equilátero.
Eso significa que el ángulo que se forma en DAB es de 60º.
Pero también podemos entender que forma parte de un triángulo equilátero de lado 10.
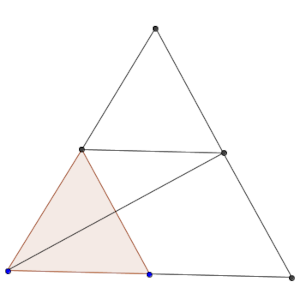
En ese sentido, la diagonal AC forma un ángulo de 90º con BC, y de 30º con AB. Eso nos va a ser de mucha utilidad.
Al ser la altura del triángulo, la distancia AC, que va a jugar un papel fundamental, se puede calcular usando el teorema de pitágoras, ya que AC² + 25 = 100. por lo que AC = raíz(75) = 5·raíz(3).
Además, cuando construimos el punto O se forma un triángulo isósceles, con lo que resulta fácil calcular la distancia entre O y A, que nos va a ser útil. Por ejemplo, por semejanza.
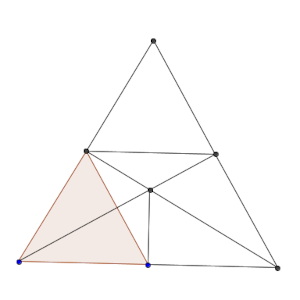
El factor de escala entre ABC y AOM, donde M es el punto medio de AB, sería AC/AM = raíz(3), por lo que AO = 10/raíz(3) = 10·raíz(3)/3.
Ahora, claramente podemos ver que la construcción del cuadrilátero AECF se puede interpretar como dos triángulos idénticos de base AC y altura OE = OF, y esa altura la podemos calcular de nuevo por semejanza.
Puesto que ABC es semejante a AEO, y sabemos que AC/AO = 3/2, tenemos que OE = 5/(3/2) = 10/3 (y OF vale lo mismo, por simetría).
Por lo tanto, el área del cuadrilátero es la suma de la de los dos triángulos, es decir, 2·(AC·OE/2) = AC·OE = 5·raíz(3)·10/3 = 50·raíz(3)/3.
También se puede abordar por coordenadas. Veamos cómo hacerlo, por construcción directa y paciencia. Juegan mucho papel los vectores de componentes raíz(3), ya que salen triángulos equiláteros.
Pondremos el eje sobre AB. A = (0, 0), B = (10, 0). Suponiendo que D = (x, y), sabemos que C = (x + 5, y). Además, debe cumplirse que x² + y² = 25 y también (x – 5)² + y² = 25, por lo que (x – 5)² = x², por lo que -10x + 25 = 0, por lo que x = 5/2. Eso significa que y² = 25 – 25/4 = 75/4, por lo que al ser positivo, y = 5·raíz(3)/2.
Tenemos ya D = (5/2, 5·raíz(3)/2), C = (15/2, 5·raíz(3)/2).
Ahora tenemos la ecuación de la recta que pasa por A y por C, raíz(3)x – 3y = 0, y tampoco es difícil sacar la ecuación de la recta BD, raíz(3)x + 3y = 10·raíz(3).
Si tratamos de cortar las dos, obtenemos que x = 5 (cosa que se aprecia por simetría), y que y = 5·raíz(3)/3. Por lo que O = (5, 5·raíz(3)/3).
Para otros cálculos, necesitamos la recta AD, raíz(3)x – y = 0, y AB, y = 0.
La perpendicular a AC que pasa por O sería 3x + raíz(3)y = 20, si la cortamos con el lado AB es F= (20/3, 0), y cortada con el lado AD, que es algo más complicado, ya que hay que hacer reducción multiplicando por raíz(3), da E = (10/3, 10·raíz(3)/3).
Es fácil ver que O es el punto medio del segmento EF, y como OE es perpendicular a AC, de nuevo dividimos el cuadrilátero en dos triángulos y calculamos 2·AC·OE/2 = 5·raíz(3)·10/3 = 50·raíz(3)/3.