Home » Olitele
Category Archives: Olitele
Solución a códigos de 10 cifras
Problema 11 del concurso Olitele 2022 Se dirige a una edad de: 16-17 años
Se ordenan aleatoriamente las cifras 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, sin repetir ninguna, para escribir un código de 10 cifras (puede comenzar por 0).
a) ¿Cuál es la probabilidad de que en ese código aparezca la cadena de números 123?
b) Cuál es la probabilidad de que en ese código, las cifras 1, 2 y 3, aparezcan en ese orden (el 1 en alguna posición antes del 2, el 2 en alguna posición antes del 3)?
Se crea un código de 10 cifras de manera que cada cifra se elige al azar entre el 0 y el 9, independientemente de las otras.
c) ¿Cuál es la probabilidad de que en ese código aparezca la cadena 20222023?
d) ¿Cuál es la probabilidad de que en ese código aparezca la cadena 2022 y también la 2023?
e) ¿Cuál es la probabilidad de que en ese código aparezca la cadena 2025?

Solución:
(more…)
Códigos de 10 cifras
Problema 11 del concurso Olitele 2022 Se dirige a una edad de: 16-17 años
Se ordenan aleatoriamente las cifras 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, sin repetir ninguna, para escribir un código de 10 cifras (puede comenzar por 0).
a) ¿Cuál es la probabilidad de que en ese código aparezca la cadena de números 123?
b) Cuál es la probabilidad de que en ese código, las cifras 1, 2 y 3, aparezcan en ese orden (el 1 en alguna posición antes del 2, el 2 en alguna posición antes del 3)?
Se crea un código de 10 cifras de manera que cada cifra se elige al azar entre el 0 y el 9, independientemente de las otras.
c) ¿Cuál es la probabilidad de que en ese código aparezca la cadena 20222023?
d) ¿Cuál es la probabilidad de que en ese código aparezca la cadena 2022 y también la 2023?
e) ¿Cuál es la probabilidad de que en ese código aparezca la cadena 2025?

Solución: Aquí.
Solución a igualdad de fracciones
Problema 10 del concurso Olitele 2022 Se dirige a una edad de: 16-17 años
Si a, b y c son tres números reales diferentes de cero que cumplen la siguiente igualdad:
(a + b)/c = (b + c)/a = (c + a)/b = R
¿Qué valor o valores reales puede tener R?
Si para un cierto valor de K (número real diferente de cero) existen tres números reales diferentes de cero a, b y c tales que
(a + Kb)/c = (b + Kc)/a = (c + Ka)/b = S
¿Para qué valores de K resulta que S puede tener un único valor?
¿Cuál es ese valor de S (y cómo depende de K)?
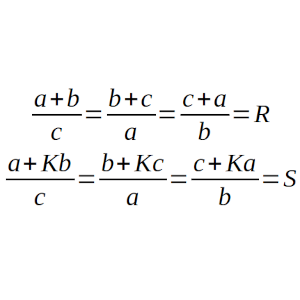
Solución:
(more…)
Igualdad de fracciones
Problema 10 del concurso Olitele 2022 Se dirige a una edad de: 16-17 años
Si a, b y c son tres números reales diferentes de cero que cumplen la siguiente igualdad:
(a + b)/c = (b + c)/a = (c + a)/b = R
¿Qué valor o valores reales puede tener R?
Si para un cierto valor de K (número real diferente de cero) existen tres números reales diferentes de cero a, b y c tales que
(a + Kb)/c = (b + Kc)/a = (c + Ka)/b = S
¿Para qué valores de K resulta que S puede tener un único valor?
¿Cuál es ese valor de S (y cómo depende de K)?
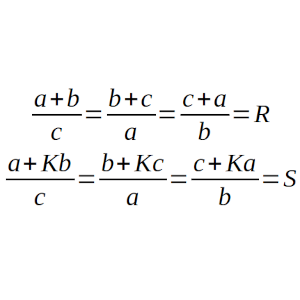
Solución: Aquí.
Solución a dividiendo un cuadrado
Problema 9 del concurso Olitele 2022 Se dirige a una edad de: 16-17 años
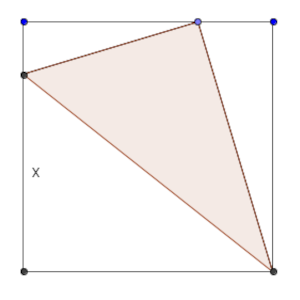
Queremos descomponer un cuadrado de 1 metro de lado en cuatro triángulos rectángulos como los indicados en la figura.
Encuentra el menor valor de x para el que es eso posible, y calcula, en caso de ser x el valor mínimo, qué área tendrá el triángulo rectángulo coloreado.
Solución:
(more…)
Dividiendo un cuadrado
Problema 9 del concurso Olitele 2022 Se dirige a una edad de: 16-17 años
Queremos descomponer un cuadrado de 1 metro de lado en cuatro triángulos rectángulos como los indicados en la figura.
Encuentra el menor valor de x para el que es eso posible, y calcula, en caso de ser x el valor mínimo, qué área tendrá el triángulo rectángulo coloreado.

Solución: Aquí.
Solución a triángulo rectángulo
Problema 7 del concurso Olitele 2022 Se dirige a una edad de: 16-17 años
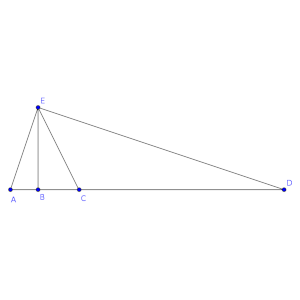
En el triángulo rectángulo AED de la figura, rectángulo en E, AB es la altura sobre la hipotenusa y EC es la bisectriz del ángulo recto.
Si se cumple que la razón de distancias entre AC y CD es 1:3, razona cuál es la proporción entre las distancias de los tres segmentos AB, BC y CD en que ha quedado dividida la hipotenusa.
Nota: seguramente no es la única manera de enfocar el problema, pero puede ser interesante que se comience por calcular la relación de distancias AB:BD.
Solución:
(more…)
Triángulo rectángulo
Problema 7 del concurso Olitele 2022 Se dirige a una edad de: 16-17 años
En el triángulo rectángulo AED de la figura, rectángulo en E, AB es la altura sobre la hipotenusa y EC es la bisectriz del ángulo recto.
Si se cumple que la razón de distancias entre AC y CD es 1:3, razona cuál es la proporción entre las distancias de los tres segmentos AB, BC y CD en que ha quedado dividida la hipotenusa.
Nota: seguramente no es la única manera de enfocar el problema, pero puede ser interesante que se comience por calcular la relación de distancias AB:BD.

Solución: Aquí.
Solución a sucesión de fracciones
Problema 6 del concurso Olitele 2022 Se dirige a una edad de: 16-17 años
Se escribe la sucesión de fracciones siguiente:
1/1, 1/2, 2/2, 1/2, 1/3, 2/3, 3/3, 2/3, 1/3, 1/4, 2/4, 3/4, 4/4, 3/4, 2/4, 1/4, …
¿Cuánto suman las fracciones que están escritas con el mismo denominador que la que ocupa la posición número 2022?
Nota: para evitar otras posibles interpretaciones, decimos que el patrón para construir la sucesión es el siguiente: se escriben todas las fracciones positivas menores que 1 de denominador n, y después la fracción n/n y a continuación las mismas fracciones en orden decreciente. Y se retoma la escritura para el siguiente valor de n.
Solución:
(more…)
Sucesión de fracciones
Problema 6 del concurso Olitele 2022 Se dirige a una edad de: 16-17 años
Se escribe la sucesión de fracciones siguiente:
1/1, 1/2, 2/2, 1/2, 1/3, 2/3, 3/3, 2/3, 1/3, 1/4, 2/4, 3/4, 4/4, 3/4, 2/4, 1/4, …
¿Cuánto suman las fracciones que están escritas con el mismo denominador que la que ocupa la posición número 2022?
Nota: para evitar otras posibles interpretaciones, decimos que el patrón para construir la sucesión es el siguiente: se escriben todas las fracciones positivas menores que 1 de denominador n, y después la fracción n/n y a continuación las mismas fracciones en orden decreciente. Y se retoma la escritura para el siguiente valor de n.

Solución: Aquí.