Home » Marató de problemes
Category Archives: Marató de problemes
Invertir las cifras
Problema 7 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
El numero 8547 tiene la característica de poderse escribir 8547 = 5862 + 2685, como suma de un número abcd de cuatro cifras, y el número de 4 cifras dcba, que resulta de invertir el orden de las cifras del anterior.
Razona cuantos números de 4 cifras tienen la característica de poderse escribir como la suma de un número de 4 cifras abcd y el número dcba que tiene las mismas cifras en orden inverso.
El número más pequeño que cumple el enunciado es el 2002 = 1001 + 1001.
Otro es el 3333, que cumple el enunciado con dos sumas con sumandos diferentes: 3333 = 1122 + 2211 = 1212 + 2121.
¿Cuál es el número más grande que cumple el enunciado? Razona cuántas sumas del tipo abcd + dcba, de dos números de cuatro cifras en el que las cifras de uno resultan de escribir en orden inverso las cifres del otro, dan como resultado este número más grande.
Razona cuántas sumas de dos números de cuatro cifras del tipo abcd + dcba dan como resultado 8547.
Solución a “Misma área, distintas proporciones”
Problema 6 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
En un triángulo ABC, trazamos dos paralelas a la base AB por dos puntos M y N del lado AC, que llegan, respectivamente a los puntos P y R del lado AB.
En el primer caso, cuando la trazamos por M, la proporción AM/MC es p y medimos el área del trapecio MABP.
En el segundo caso, medimos el área del triángulo NRC, y resulta ser la misma que la del anterior trapecio. ¿Qué proporción AN/NC hay?
Solución:
(more…)Solución a “Valores absolutos”
Problema 5 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
Si a, b y c pueden tener como valor tres números reales, diferentes todos ellos de 0, y |x| representa el valor absoluto de x, se pide obtener cuántos valores diferentes puede tener la expresión 4·a/|a|+ 3·b/|b| + 2·c/|c| + a·b/|a·b| + b·c/|b·c| + c·a/|c·a|.
Solución:
(more…)Valores absolutos
Problema 5 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
Si a, b y c pueden tener como valor tres números reales, diferentes todos ellos de 0, y |x| representa el valor absoluto de x, se pide obtener cuántos valores diferentes puede tener la expresión 4·a/|a|+ 3·b/|b| + 2·c/|c| + a·b/|a·b| + b·c/|b·c| + c·a/|c·a|.
Solución: Aquí.
Solución a “Recipiente”
Problema 4 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
Un recipiente está formado por un cilindro y un cono unidos, con una altura total de 50 cm, y contiene cierto líquido.
Cuando el recipiente está en posición vertical y el cilindro está en la parte inferior, el líquido llega a una altura de 22 cm.
Sin embargo, si se coloca con el cono en la parte inferior, el líquido alcanza una altura de 39 cm.
¿Qué parte del recipiente (expresado como fracción irreducible) ocupa el líquido que contiene?
Solución:
(more…)Recipiente
Problema 4 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
Un recipiente está formado por un cilindro y un cono unidos, con una altura total de 50 cm, y contiene cierto líquido.
Cuando el recipiente está en posición vertical y el cilindro está en la parte inferior, el líquido llega a una altura de 22 cm.
Sin embargo, si se coloca con el cono en la parte inferior, el líquido alcanza una altura de 39 cm.
¿Qué parte del recipiente (expresado como fracción irreducible) ocupa el líquido que contiene?
Solución: Aquí.
Solución a “Capicúa”
Problema 3 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
Ariadna ha de sumar el conjunto de los 125 números capicúas de 5 cifras en los que todas y cada una de las cifras que los forman son impares.
Sin embargo, a la hora de calcular la suma se ha dejado uno de los números y sólo ha sumado 124.
Ha obtenido el número 6 913 262.
¿Cuál es el número que no ha sumado?
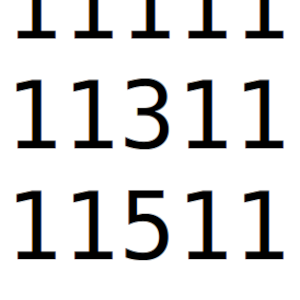
Solución:
(more…)
Capicúa
Problema 3 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
Ariadna ha de sumar el conjunto de los 125 números capicúas de 5 cifras en los que todas y cada una de las cifras que los forman son impares.
Sin embargo, a la hora de calcular la suma se ha dejado uno de los números y sólo ha sumado 124.
Ha obtenido el número 6 913 262.
¿Cuál es el número que no ha sumado?
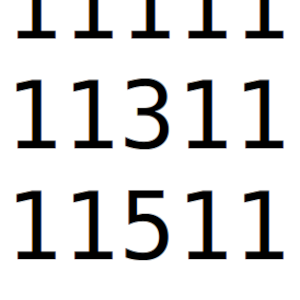
Solución: Aquí.
Solución a “De hexágono a triángulo”
Problema 2 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
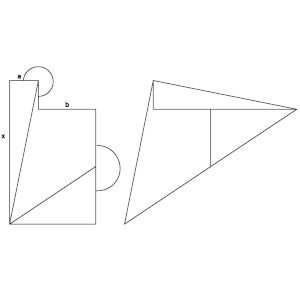
El hexágono de la izquierda tiene todos los ángulos rectos, y las longitudes de dos lados son a y b, tal y como está indicado en la figura.
Si dividimos el hexágono en las tres partes que muestra la figura y las giramos adecuadamente, podemos componer un triángulo.
Expresa la longitud x, que corresponde al lado izquierdo del polígono inicial, en función de a y b.
(Por si es demasiado pequeño, aclaro que a y b son las longitudes de los dos lados horizontales superiores del hexágono.)
Solución:
(more…)
De hexágono a triángulo
Problema 2 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
El hexágono de la izquierda tiene todos los ángulos rectos, y las longitudes de dos lados son a y b, tal y como está indicado en la figura.
Si dividimos el hexágono en las tres partes que muestra la figura y las giramos adecuadamente, podemos componer un triángulo.
Expresa la longitud x, que corresponde al lado izquierdo del polígono inicial, en función de a y b.
(Por si es demasiado pequeño, aclaro que a y b son las longitudes de los dos lados horizontales superiores del hexágono.)
Solución: Aquí.