Problema 2 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
Sea P(x) un polinomio de grado 5, y sean a y b dos números reales diferentes de 0.
Supongamos que el resto de P(x) al dividirlo por x³ + ax + b es igual al resto al dividirlo por x³ + ax² + b.
Determinar el valor de a + b.
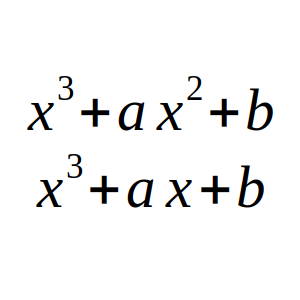
Solución:
Continue reading Solución a “Dos polinomios muy parecidos”