Problema 4 de la Olitele (Olimpiada Telemática de Cataluña) 2017 Se dirige a una edad de: 16-17 años
En un pentágono inscrito en una circunferencia ABCDE trazamos las diagonales AD y BE, que se cortan en F.
Suponiendo conocidos los ángulos internos del pentágono en A (BAE), en E (AED) y en C (DCB), calcular el ángulo entre las diagonales AFB.
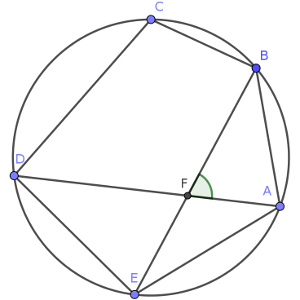
Solución:
En estos problemas de geometría, en los que aparece una circunferencia, es fundamental conocer la propiedad del ángulo central. El ángulo desde el centro hacia un segmento mide el doble que desde cualquier punto de una circunferencia, pero siempre que se mida en el mismo sentido. Eso quiere decir que si estamos al otro lado del segmento, desde otro punto de la circunferencia no medirá lo mismo el ángulo, medirá el suplementario (sumará 180 grados con el del otro lado).
En este caso, el ángulo DCB suma 180 grados con los ángulo DEB y DAB, puesto que A y E están al otro lado del segmento DB, y ahí está la clave.
Otra manera diferente de abordar el problema es trazar todos los radios desde el centro, generar triángulos isósceles (pues todos los radios miden lo mismo), y razonar con los ángulos que se construya con ellos, pero será mucho más costoso. Es equivalente, ya que la propiedad a a la que hacemos referencia se puede deducir de la existencia de estos triángulos.
El caso es que para conseguir ese ángulo, podemos tratar de conseguir AFE.
Vamos a marcar los ángulos conocidos. El valor de DCB es c, el valor de AED es e y el valor de BAE es a. Por estar en una circunferencia, DEB vale 180 – c y también DAB mide lo mismo. Como e = DEB + FEA, podemos tener que FEA es e + c – 180, y de la misma forma FAE es a + c – 180.
Como A, F y E forman un triángulo, sus tres ángulos suman 180 grados, así que 180 = AFE + e + c – 180 + a + c – 180 = AFE + a + e + 2c – 360. De ahí, deducimos que AFE = 540 – a – e – 2c.
Como AFB y AFE suman 180, tenemos que 180 = 540 – a – e – 2c + x, de forma que x = a + e + 2c – 360, medido en grados.
Es decir, que el ángulo buscado será el resultado de quitar una vuelta completa a la suma de los ángulos internos de A, B y dos veces C.