Problema 11 de la Olitele (Olimpiada Telemática de Cataluña) 2017 Se dirige a una edad de: 16-17 años
En una bolsa hay n bolas, en cada una de las cuales hay escrito un número natural.
Hacemos el experimento aleatorio de extraer dos bolas de esa bolsa y sumar los números que aparecen.
Designamos como p la probabilidad de que la suma de ambos números sea par, y q la probabilidad de que sea impar.
Estudia cuáles pueden ser los valores de n y qué distribución han de tener los números de la bolsa para que se cumpla que p = q.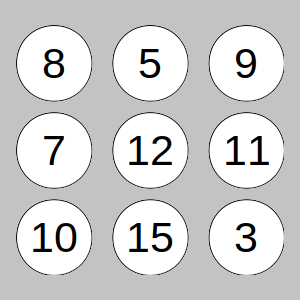
Solución:
Se trata de un problema más interesante de lo que parece.
En un principio, debemos intentar probar pequeñas combinaciones para ver qué funciona o qué no.
Puesto que sólo nos interesa si la suma es par o impar, lo único que nos preocupa es la paridad de los números dibujados en las bolas, ya que la suma de dos pares cualesquiera siempre es par, la de dos impares siempre es par, y si sumamos una impar y una par siempre obtenemos par.
De forma que únicamente nos ocuparemos de cuántas de las n bolas sean pares y cuántas impares.
Por otra parte, que la suma sea par o sea impar es todo lo que puede pasar, es decir, no hay una tercera opción, por lo que está claro que p + q vale 1 y si son iguales, ambos valen ½.
Vamos a investigar lo que sucede para pequeños valores. Si únicamente hay dos bolas, el experimento tiene poco interés, ya que la suma siempre dará lo mismo, y o bien p o q será 1 y el otro 0, no podrán ser iguales.
Si hay tres, supongamos que hay dos de un tipo y una del otro (el otro caso es muy aburrido). La primera bola que observemos tiene ⅓ de probabilidad de ser de un cierto tipo y ⅔ del tipo contrario. Si estamos en el primer caso, con seguridad la segunda será del tipo contrario, mientras que en el otro caso tenemos un 50% de probabilidad de ambos casos. Por lo tanto, la suma será par con un 0% de probabilidad en el primer caso y con ⅓ en el segundo, es decir, será par con p = ⅓. El valor de q lo obtenemos sumando ⅓ del primer caso con ⅓ del segundo, ⅔.
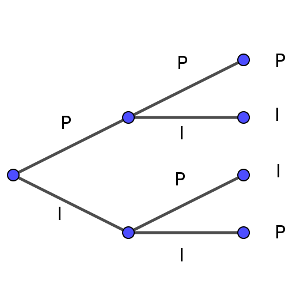
Una vez entendido cómo se ha hecho el cálculo, aunque esta vez sea infructuoso, estamos en disposición de realizar el cálculo teórico. La decisión que habrá que tomar es hacer depender todo de, por ejemplo, n y la cantidad de bolas pares, o bien de la cantidad de bolas pares y la cantidad de bolas impares. En una primera aproximación lo hice de una forma y la expresión no me proporcionó suficiente información. Volver a empezar con las otras variables hizo que me diera cuenta de la clave. Y ahora podría razonarlo con las dos expresiones.
Supongamos que llamamos a a la cantidad de bolas con un número par y b a la cantidad de bolas con un número impar. Evidentemente, n = a + b.
La primera bola que observemos es par con una probabilidad de a/(a + b). Suponiendo que ésto es así, la probabilidad de que la segunda sea impar será de b/(a + b – 1), ya que queda una bola menos entre las que escoger. Por lo tanto la probabilidad de que suceda esta situación será el producto ab/((a + b)(a + b – 1)).
Puesto que la probabilidad de que la primera sea impar es b/(a + b) y la de que, siendo así, la segunda sea par es de a/(a + b – 1), la probabilidad de que suceda esta otra situación será idéntica, ab/((a + b)(a + b – 1)).
Como la probabilidad de que sea impar es la suma de estas dos únicas situaciones (ver árbol de decisión), tendremos que q = 2ab/((a + b)(a + b – 1)).
Para que p = q, hemos dicho que basta que q valga ½, de forma que se debe dar 1/2 = 2ab/((a + b)(a + b – 1)). Quitando denominadores nos queda que (a + b)(a + b – 1) = 4ab.
Ahora, desarrollando la expresión del paréntesis, tenemos que a² + 2ab + b² – a – b = 4ab, e igualando a cero, tenemos que a² – 2ab + b² – a – b = 0.
Ahora viene la idea genial, ya que a y b debe ser entero, por lo que a² – 2ab + b² = a + b, es decir, (a – b)² = n.
Y aquí viene la interpretación. Eso quiere decir que, si queremos que p y q sean iguales, n debe ser un cuadrado perfecto (evidentemente, mayor que uno, si queremos poder sacar dos bolas), y la diferencia entre bolas pares e impares debe ser su raíz. Supongamos que n = k² , puesto que a + b = k² y a – b = k, es sencillo ver que o bien a = (k² + k)/2, y b = (k² – k)/2, o bien a la inversa, ya que (b – a)² = (a – b)².
Por ejemplo, podemos tomar 4 bolas, de forma que haya una impar y tres pares, o bien nueve bolas de forma que haya 6 impares y 3 pares, como en el dibujo. Podemos comprobar que la probabilidad de que la suma de dos tomados al azar sea par o impar es exactamente ½.