Problema 5 de la Fase Local (sábado) de la Olimpiada Matemática Española (2018)
Se dirige a una edad de: 16-17 años

Sean a, b y c números naturales primos, distintos dos a dos.

Demuestra que el número (ab)^{c – 1} + (bc)^{a – 1} + (ac)^{b – 1} – 1 es un múltiplo del producto abc.

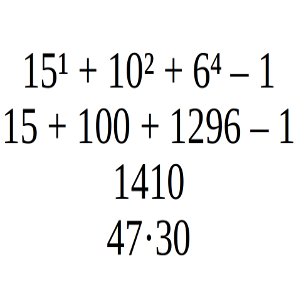
Solución:

Las únicas pruebas con las que podemos trabajar son números relativamente grandes, y aparentemente no dan pistas para abordar el problema. La más baja es la que corresponde a los números primos 2, 3 y 5, y el número que resulta es de cuatro cifras.

Una cosa que es fácil de deducir es que debemos trabajar la divisibilidad de cada uno de los primos por separado. Puesto que son primos diferentes, si el número que estudiamos es divisible por los tres, también lo será por su producto.

Supongamos que queremos estudiar la divisibilidad de la expresión (ab)^c-1 + (bc)^a-1 + (ac)^b-1 – 1 entre el primo a, ya que dada la simetría de la expresión será igual de sencillo (o de complicado) comprobar la divisibilidad entre cualquier otro de los dos primos.

En esa suma de cuatro términos, tanto (ab)^c-1 como (ac)^b-1 son claramente múltiplos de a, ya que las potencias son de exponente mayor o igual que 1, pero está claro que (bc)^a-1 no lo es. Debemos ver que (bc)^a-1 – 1 es múltiplo de a, y entonces estará completa la demostración.

Salvo que hayamos estudiado congruencias, este resultado me parece muy difícil para estudiantes de secundaria, ya que se trata de un caso particular del llamado Pequeño Teorema de Fermat.

En realidad, cualquier número n que no sea múltiplo de a cumple que n^a-1 – 1 es divisible por a. Voy a trabajar una demostración indirecta para explicarlo, pero insisto que si no se ha visto con anterioridad me parecería muy difícil que un estudiante lo dedujese sobre la marcha.

Vamos a trabajar con la expresión n^a – n y comprobar que es divisible por a para cualquier valor de n. Puede parecer que no tiene nada que ver, pero hay que tener un poco de paciencia.

Está claro que es cierto si n = 1, ya que en ese caso vale 0. Ahora bien, si pensamos que ese resultado es cierto para la cadena de números 1, 2, … , n ¿podríamos verificarlo para el siguiente, n + 1?

Veamos, (n + 1)^a – (n + 1) = n^a + a·n^a-1 + (a·(a – 1))/2)·n^a-2 + … + a·n + 1 – (n + 1). El desarrollo de esta potencia se trabaja en primero de bachillerato, y todos sus sumandos, excepto el primero y el último, tienen un coeficiente que se obtiene multiplicando secuencias de números consecutivos (que empiezan por a) y dividiendo entre otra secuencia de la misma cantidad de números consecutivos (que acaban en 1). Está claro que el factor a nunca se simplificará, ya que es primo (no se puede dividir por ningún número menor), y puesto que el resultado es un número entero, va a tratarse de un múltiplo de a (excepto en el caso del primer y el último términos, que llevan el coeficiente 1).

Por lo tanto, (n + 1)^a – (n + 1) = n^a + (múltiplo de a) + 1 – (n + 1) = n^a – n + múltiplo de a.

Pero este valor, n^a – n, hemos supuesto que es múltiplo de a, por lo que también lo es (n + 1)^a – (n + 1).

Por lo tanto, n^a – n = n(n^a-1 – 1) siempre es múltiplo de a, y, claro, cuando n no es múltiplo de a, debe ser que n^a-1 – 1 sí es múltiplo de a, porque al multiplicarlo por n obtenemos un múltiplo de a.

Se trata de una demostración muy curiosa, pero que nos da muchas pistas para tratar con potencias de números en términos de divisibilidad. Espero que al menos este problema haya servido para esto.

El caso es que, en nuestro problema, es evidente que bc no es múltiplo de a, de forma que (bc)^a-1 – 1 sí que es múltiplo de a, y por tanto la expresión inicial debe, en cualquier caso, ser múltiplo de a. De la misma forma, es múltiplo de b y de c, logrando que sea múltiplo de abc.

Observamos que para números compuestos no vale casi nada de lo expuesto, ya que el resultado de Fermat usa el hecho de que sea primo, y el razonamiento por factores también.