Problema 5 del primer nivel la Olimpiada de Mayo (2017)
Se dirige a una edad de: 12 años

Diremos que dos números enteros a y b forman una pareja adecuada si a+b divide a ab (su suma divide a su multiplicación.

Hallar 24 números que se puedan distribuir en 12 parejas adecuadas, de modo que cada número figure en una única pareja y el mayor de los enteros sea lo menor posible.

Solución:

En este ejercicio la primera dificultad consiste en encontrar un método rápido para conseguir parejas adecuadas, de forma que podamos construir o seleccionar entre los enteros rápidamente doce parejas de números distintos.

Una clave en la que nos podemos fijar es, que si tomamos el mayor divisor común de la pareja adecuada, tendremos que el producto tendrá este factor al cuadrado. Está claro que la suma tiene factor común este mismo factor, y la suma de los otros dos factores debe dividir al producto de los dos números. Claro, que si divide a el factor común, dividirá al producto seguro. Si no es así (si esa suma no divide al producto) debería dividir a alguno de los otros factores de uno de los dos números, cosa que es imposible, ya que si tenemos un factor primo que divida a uno de los dos sumandos, pero no al otro, la suma de los dos no puede ser dividida por ese factor.

Así, una manera muy simple de encontrar números adecuados es tomar dos números primos entre sí y multiplicarlos por múltiplos de su suma.

Puesto que 1 + 2 = 3, 3 y 6 forman la pareja adecuada menor posible. Otras parejas adecuadas familia de esta suma serían 6 y 12 (repetiríamos el 6), 9 y 18, 12 y 24, 15 y 30, 18 y 36, 21 y 42, 24 y 48 y así sucesivamente.

También 1 + 3 = 4, de forma que tenemos 4 y 12, 8 y 24, 12 y 36, 16 y 48, …

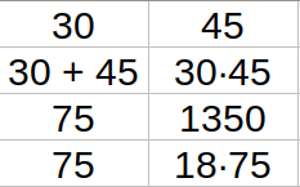
Ahora, 2 + 3 = 5, por lo que tenemos 10 y 15, 20 y 30, 30 y 45,…

También 1 + 4 = 5, y tenemos 5 y 20, 10 y 40, …

Puesto que 1 + 5 = 6, tenemos 6 y 30, …

Con suma 7, tenemos 1+6, por lo que estaría el 7 y 42.

También con 7, 2 + 5, que daría el 14 y el 35.

Y con 7 estaría el 3 + 4, es decir que sería el 21 y el 28.

También con suma 8, el 3 y el 5, tendría el 24 y el 42, es el único por debajo de 50.

Con suma 9, el 4 + 5, que da el 36 y el 45.

Ya no es necesario tomar más ejemplos, ya que mirando por debajo del 50 podemos tomar 12 parejas (buscando no repetir números, aunque es difícil seleccionarlas). Las ordenamos de forma que el número mayor sea el menor posible, y tenemos 3 – 6, 4 – 12, 9 – 18, 5 – 20, 8 – 24, 21 – 28, 15 – 30, 14 – 35, 10 – 40, 7 – 42, 36 – 45, y 16 – 48.

En resumen, si elegimos el conjunto de 24 números (por orden) 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 24, 28, 30, 35, 36, 40, 42, 45 y 48 se cumplen todas las condiciones. Por debajo del 48 es imposible, porque hay pocas parejas de números. Aunque llegan a superar a 12 el número de parejas, usan muchos números repetidos, y son menos de 24.

En efecto, si tomamos todas las parejas de números adecuados por debajo de 48 son exactamente 21 parejas, pero sólo usan 22 números, (3, 4, 5, 6 (3 veces), 7, 8, 9, 10 (2 veces), 12 (4 veces), 14, 15 (2 veces), 18 (2 veces), 20 (2 veces), 21 (2 veces), 24 (3 veces), 28, 30 (4 veces), 35, 36 (3 veces), 40 (2 veces), 42 (2 veces), y 45 (2 veces)). La lista la hice pacientemente poniendo todos los números ordenados y sumando las veces que se repetían (ponía una marca junto al número). Así se puede comprobar que se anotan 42 marcas.

Evidentemente, es necesario incluir todas las parejas de aquellos números que se repitan una única vez y marcar como utilizadas todas las parejas que incluyan a su pareja adecuada. Hay una única manera de tomar estos 22 números para formar 11 parejas adecuadas. Luego, basta tomar una pareja que use el 48 y que no utilice ningún número usado anteriormente, que debe ser el 16.

Se trata de un problema complejo, en el que es necesario ser paciente y ordenado para cumplir todos los requisitos.