Problema 3 del primer nivel de la Olimpiada de Mayo (2018) Se dirige a una edad de: 12 años
Sea ABCDEFGHIJ un polígono regular de 10 lados que tiene todos sus vértices en un polígono regular de centro O y radio 5.
Las diagonales AD y BE se cortan en P, y las diagonales AH y BI se cortan en Q.
Calcular la medida del segmento PQ.
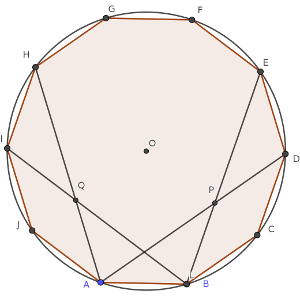
Solución:
Se trata de un problema complicado de resolver a este nivel, pero muy bonito porque busca relaciones entre ángulos y simetrías.
El primer problema que encontramos es dibujar, aunque sea a mano alzada, un borrador de la situación. Un sistema para acabar rápido es dibujar un pentágono regular, aunque sea de forma aproximada, y dibujar la circunferencia que lo contiene. Dividiendo en dos los arcos entre las figuras, tenemos rápido algo parecido a un decágono regular (si la persona que se enfrenta al problema conoce la técnica para dibujar con regla y compás un pentágono regular, quedará mucho mejor acabado, claro).
Una vez que hemos acabado, es sencillo localizar cuáles son las diagonales que nos interesan.
Dada la simetría de la situación, rápidamente podemos observar que los radios OJ y OC contienen, por simetría, los puntos Q y P, respectivamente.

Rápidamente, al unir estos puntos, observamos que el polígono ABPOQ parece un pentágono regular.
Si conseguimos razonar que en efecto lo es, la distancia PQ será una de las diagonales, y coincidiría con cualquiera de las otras, en particular con OA y OB, que son ambas radios de la circunferencia.
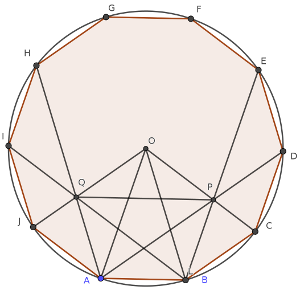
Por lo tanto, puesto que el radio de la circunferencia mide 5, tendríamos que la medida de PQ es exactamente 5. ¿Cómo podríamos justificar que todos los ángulos del polígono valen lo mismo (la simetría de la figura obligaría a que los lados también midiesen lo mismo en ese caso)?
Una idea sencilla sería trabajar con el ángulo inscrito, que es doble que el central. Puesto que el ángulo desde el que se ve un lado del decágono desde el centro es siempre 36º, desde el borde de la circunferencia cualquier lado se ve bajo un ángulo de 18º, por lo que el ángulo COJ sería de 108º (el triple de un lado), mientras que EBA, igual que HAB miden también 108º, por abarcar seis veces un ángulo de un lado. Puesto que los otros dos ángulos son iguales, por la suma total también deben medir lo mismo (en un pentágono los ángulos interiores suman 180º*3 = 540º), y confirmaríamos el supuesto.
Pero en este nivel no suelen tener ese conocimiento, así que vamos a dar otro enfoque más largo, pero válido también.
Empecemos pensando que, si unimos todos los vértices con el centro de la circunferencia, los triángulos isósceles tendrán el ángulo menor de la décima parte de 360º, es decir, 36º. Y los otros dos, al tener que sumar 180º con 36º, deben medir 72º cada uno. Eso quiere decir que los ángulos del borde del decágono regular miden 144º.
En todos los cuadriláteros, los ángulos interiores deben sumar 360º, ya que siempre se pueden dividir en dos triángulos. En los casos de los trapecios BCDE y AJIH, puesto que tienen dos ángulos de 144º y está claro que son simétricos, los otros dos ángulos deben ser iguales, por lo que deben de medir todos 36º. De esta forma, por ejemplo, sabemos que el ángulo CBP debe medir 36º.
Por lo tanto, ABE (y también BAH) está claro que debe medir 144º – 36º = 108º, que era lo que buscábamos.
Además, ya que OC es un radio, divide el ángulo BCD por la mitad, de forma que el triángulo BPC tiene ángulos 36º, 72º, 72º y es isósceles. Por tanto, BPO, que es igual que AQO, debe medir 180º – 72º = 108º también.
Por último, por formar un pentágono, el ángulo restante también debe medir lo mismo, y la simetría de la figura nos permite razonar que las medidas de los lados también son iguales (por ejemplo, también razonaríamos por triángulos isósceles).
De forma que, en efecto, la medida de PQ debe ser, en efecto, 5.