Problema 4 del primer nivel de la Olimpiada de Mayo (2018) Se dirige a una edad de: 12 años
Ana debe escribir 7 enteros positivos, no necesariamente distintos, alrededor de una circunferencia de manera que se cumplan las siguientes condiciones:
La suma de los siete números es igual a 36.
Si dos números son vecinos la diferencia entre el mayor y el menor es igual a 2 o 3.
Hallar el máximo valor del mayor de los números que puede escribir Ana.
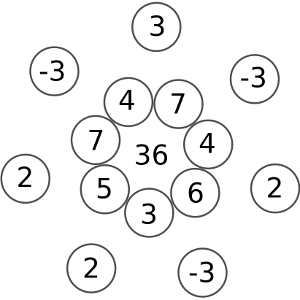
Solución:
Es un problema que pone a prueba la paciencia de los participantes en esta prueba, ya que necesita un estudio bastante largo para buscar soluciones, y no es fácil usar atajos (como el álgebra) para acelerar el proceso.
Al principio, opté por el tanteo pero luego, pensando en las diferencias, llegué a la conclusión de que, mirando en uno de los sentidos, puesto que tenía que dar la vuelta completa a la circunferencia, las diferencias debían anularse (es decir, las positivas y las negativas).
Como además son una cantidad impar de números, no pueden ser todas las diferencias iguales.
Como hacen falta dos treses para compensar tres doses, las diferencias deben ser, por ejemplo, 2, 2, 2, -3, -3, y dos sumandos más que se compensen (dos doses o dos treses, de signos opuestos). Además, podemos pensar que empezamos por el número más bajo, y por tanto el total de las diferencias nunca puede ser negativo.
El número menor lo empecé fijando a 1, porque si aumentamos ese manteniendo las diferencias, sería como aumentar todos uno, con lo que la suma alcanzaría siete unidades más.
Por ejemplo, si utilizo la secuencia +2, +2, +2, -3, +2, -2, -3, me lleva a la secuencia de números 1, 3, 5, 7, 4, 6, 4, que suma 30. Pero si empiezo desde 2, tengo 2, 4, 6, 8, 5, 7, 5, que suma 37.
Cambiar la secuencia a +2, +2, +2, +2, -3, -2, -3, lleva a 1, 3, 5, 7, 9, 6, 4, que suma 35.
Es difícil encontrar una combinación que sume 36, por ejemplo, +2, +2, +2, +2, -2, -3, -3, lleva a 1, 3, 5, 7, 9, 7, 4, que suma 36. Y el valor mayor es, en este caso, 9.
La secuencia +3, +3, +3, -3, -2, -2, -2, lleva a 1, 4, 7, 10, 7, 5, 3, que suma 37.
Otra combinación interesante es la secuencia +3, -2, +3, +3, -2, -3, -2, que lleva a 1, 4, 2, 5, 8, 6, 3, que suma 29. Y por tanto, 2, 5, 3, 6, 9, 7, 4 suma 36. Y también tiene 9 como número mayor.
La secuencia +3, -2, +3, -3, +3, -2, -2, lleva a 1, 4, 2, 5, 2, 5, 3, que suma 22. Si aumentamos 2 el de partida, llegamos a 3, 6, 4, 7, 4, 7, 5, que suma 36 y en esta ocasión el mayor es 7.
Hemos encontrado dos combinaciones que suman 36, y tienen por número mayor 9. ¿Será ésta la respuesta correcta? Tengamos en cuenta que la única secuencia que hemos obtenido que tiene un 10 suma 37, y por tanto no es válida, aunque está muy próxima.
Es difícil, aunque posible, agotar todas las combinaciones y explorar todas las posibilidades.
Vamos a ir por un camino algo más retorcido, pero más corto. Supongamos que el número mayor es mayor o igual que 10. Los números adyacentes deben ser al menos 7, si uno de ellos fuese 8, entre los tres sumarían al menos 25, y los dos junto a ellos deberían ser al menos 4 y 5, y ya sumarían al menos 34. Los demás no pueden ser dos unos, pues su diferencia estaría por debajo del mínimo. Luego el mayor valor posible es 10 y los dos adyacentes serán 7, y por eso los dos que hay junto a ellos deberían ser 4 o 5. Si ambos fuesen 5, los dos que faltan deberían ser 1, lo cual es imposible, si uno de ellos es 4 y el otro 5, los que sobran deben sumar 3, es decir que uno de ellos debe ser 1 y el otro 2, y no pueden guardar la distancia de 2, y si ambos son 4, la suma de los dos que cierran el círculo debería ser 4, que nos deja como única posibilidad que ambos fuesen 2, lo que tampoco da la distancia adecuada.
Por lo tanto, según hemos visto, el mayor valor posible es 9.
No me quedé satisfecho con la resolución, así que inicié una hoja en la que puse todas las combinaciones posibles de diferencias, a qué números llevan, y la suma más próxima a 36 (por debajo), de forma que descubrí que hay 39 posibles grupos de diferencias, de los cuales 4 dan lugar a valores repetidos (porque tienen dos posiciones mínimas, y unas empiezan en uno y otras en otro). De esos 35 valores diferentes, sólo 5 pueden llegar a sumar 36, y son los siguientes:
3 5 7 4 7 4 6 36
2 4 7 4 6 8 5 36
2 4 7 9 6 3 5 36
2 4 6 8 5 7 4 36
1 3 5 7 9 7 4 36
La tabla completa, la dejo a continuación. Los primeros siete números son las diferencias, tratando de situar primero las menores, pero sin bajar nunca del mínimo. A continuación, a qué números llevan si empezamos con el 1, lo que suma, y la suma más próxima a 36 por debajo que podríamos lograr si empezáramos con otro entero.
|
2 |
2 |
-3 |
2 |
-3 |
3 |
-3 |
1 |
3 |
5 |
2 |
4 |
1 |
4 |
20 |
34 |
|
|
2 |
2 |
-3 |
2 |
3 |
-3 |
-3 |
1 |
3 |
5 |
2 |
4 |
7 |
4 |
26 |
33 |
|
|
2 |
2 |
-3 |
3 |
-3 |
2 |
-3 |
1 |
3 |
5 |
2 |
5 |
2 |
4 |
22 |
36 |
|
|
2 |
2 |
-3 |
3 |
2 |
-3 |
-3 |
1 |
3 |
5 |
2 |
5 |
7 |
4 |
27 |
34 |
|
|
2 |
2 |
2 |
-3 |
-3 |
3 |
-3 |
1 |
3 |
5 |
7 |
4 |
1 |
4 |
25 |
32 |
|
|
2 |
2 |
2 |
-3 |
3 |
-3 |
-3 |
1 |
3 |
5 |
7 |
4 |
7 |
4 |
31 |
31 |
|
|
2 |
2 |
2 |
3 |
-3 |
-3 |
-3 |
1 |
3 |
5 |
7 |
10 |
7 |
4 |
37 |
30 |
|
|
2 |
2 |
3 |
-3 |
-3 |
2 |
-3 |
1 |
3 |
5 |
8 |
5 |
2 |
4 |
28 |
35 |
|
|
2 |
2 |
3 |
-3 |
2 |
-3 |
-3 |
1 |
3 |
5 |
8 |
5 |
7 |
4 |
33 |
33 |
|
|
2 |
2 |
3 |
2 |
-3 |
-3 |
-3 |
1 |
3 |
5 |
8 |
10 |
7 |
4 |
38 |
31 |
|
|
2 |
3 |
-3 |
2 |
-3 |
2 |
-3 |
1 |
3 |
6 |
3 |
5 |
2 |
4 |
24 |
31 |
|
|
2 |
3 |
-3 |
2 |
2 |
-3 |
-3 |
1 |
3 |
6 |
3 |
5 |
7 |
4 |
29 |
36 |
|
|
2 |
3 |
2 |
-3 |
-3 |
2 |
-3 |
1 |
3 |
6 |
8 |
5 |
2 |
4 |
29 |
36 |
|
|
2 |
3 |
2 |
-3 |
2 |
-3 |
-3 |
1 |
3 |
6 |
8 |
5 |
7 |
4 |
34 |
34 |
|
|
2 |
3 |
2 |
2 |
-3 |
-3 |
-3 |
1 |
3 |
6 |
8 |
10 |
7 |
4 |
39 |
32 |
|
|
3 |
-3 |
2 |
2 |
-3 |
2 |
-3 |
REP |
|||||||||
|
3 |
-3 |
2 |
2 |
2 |
-3 |
-3 |
REP |
|||||||||
|
3 |
2 |
-3 |
2 |
-3 |
2 |
-3 |
1 |
4 |
6 |
3 |
5 |
2 |
4 |
25 |
32 |
|
|
3 |
2 |
-3 |
2 |
2 |
-3 |
-3 |
1 |
4 |
6 |
3 |
5 |
7 |
4 |
30 |
30 |
|
|
3 |
2 |
2 |
-3 |
-3 |
2 |
-3 |
1 |
4 |
6 |
8 |
5 |
2 |
4 |
30 |
30 |
|
|
3 |
2 |
2 |
-3 |
2 |
-3 |
-3 |
1 |
4 |
6 |
8 |
5 |
7 |
4 |
35 |
35 |
|
|
3 |
2 |
2 |
2 |
-3 |
-3 |
-3 |
1 |
4 |
6 |
8 |
10 |
7 |
4 |
40 |
33 |
|
|
2 |
-2 |
2 |
2 |
-3 |
2 |
-3 |
1 |
3 |
1 |
3 |
5 |
2 |
4 |
19 |
33 |
|
|
2 |
-2 |
2 |
2 |
2 |
-3 |
-3 |
1 |
3 |
1 |
3 |
5 |
7 |
4 |
24 |
31 |
|
|
2 |
2 |
-3 |
2 |
-3 |
2 |
-2 |
REP |
|||||||||
|
2 |
2 |
-3 |
2 |
-2 |
2 |
-3 |
1 |
3 |
5 |
2 |
4 |
2 |
4 |
21 |
35 |
|
|
2 |
2 |
-3 |
2 |
2 |
-3 |
-2 |
1 |
3 |
5 |
2 |
4 |
6 |
3 |
24 |
31 |
|
|
2 |
2 |
-3 |
2 |
2 |
-2 |
-3 |
1 |
3 |
5 |
2 |
4 |
6 |
4 |
25 |
32 |
|
|
2 |
2 |
-2 |
2 |
-3 |
2 |
-3 |
1 |
3 |
5 |
3 |
5 |
2 |
4 |
23 |
30 |
|
|
2 |
2 |
-2 |
2 |
2 |
-3 |
-3 |
1 |
3 |
5 |
3 |
5 |
7 |
4 |
28 |
35 |
|
|
2 |
2 |
2 |
-3 |
-3 |
2 |
-2 |
REP |
|||||||||
|
2 |
2 |
2 |
-3 |
-2 |
2 |
-3 |
1 |
3 |
5 |
7 |
4 |
2 |
4 |
26 |
33 |
|
|
2 |
2 |
2 |
-3 |
2 |
-3 |
-2 |
1 |
3 |
5 |
7 |
4 |
6 |
3 |
29 |
36 |
|
|
2 |
2 |
2 |
-3 |
2 |
-2 |
-3 |
1 |
3 |
5 |
7 |
4 |
6 |
4 |
30 |
30 |
|
|
2 |
2 |
2 |
-2 |
-3 |
2 |
-3 |
1 |
3 |
5 |
7 |
5 |
2 |
4 |
27 |
34 |
|
|
2 |
2 |
2 |
-2 |
2 |
-3 |
-3 |
1 |
3 |
5 |
7 |
5 |
7 |
4 |
32 |
32 |
|
|
2 |
2 |
2 |
2 |
-3 |
-3 |
-2 |
1 |
3 |
5 |
7 |
9 |
6 |
3 |
34 |
34 |
|
|
2 |
2 |
2 |
2 |
-3 |
-2 |
-3 |
1 |
3 |
5 |
7 |
9 |
6 |
4 |
35 |
35 |
|
|
2 |
2 |
2 |
2 |
-2 |
-3 |
-3 |
1 |
3 |
5 |
7 |
9 |
7 |
4 |
36 |
36 |