Problema 4 de la Fase Nacional de la XLVII OME 2011 Se dirige a una edad de: 16-17 años
Sea ABC un triángulo con un ángulo en A que es doble del ángulo en B, y un ángulo en C mayor de 90º.
Sea D un punto de la recta AC tal que BD es perpendicular a BC, y M el punto medio de AB.
Demuestra que el ángulo AMC coincide con el ángulo DMB.
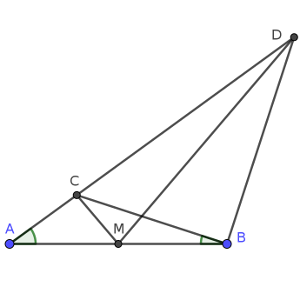
Solución:
Este problema lo incluyo ahora porque su construcción inicial no parece ser muy distinto del anterior, pero la resolución no es fácil llevarla a cabo de manera similar.
Por supuesto, podríamos intentar una estrategia que se base en construir elementos utilizando el teorema del seno y del coseno, partiendo del valor de la mitad del lado AB, que tomaríamos como unidad. Haciendo depender todo en ese momento del ángulo menor (el CBA), construir CA, CM, el coseno del ángulo BMA, DB, DM y así obtener el coseno del ángulo DMB, que debe coincidir con el anterior. En teoría debe funcionar, pero no es en absoluto viable llevarlo a cabo.
Hay una aproximación mucho más retorcida, pero muy sencilla de entender cuando te das cuenta.
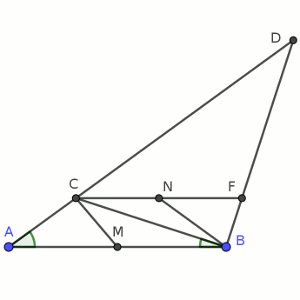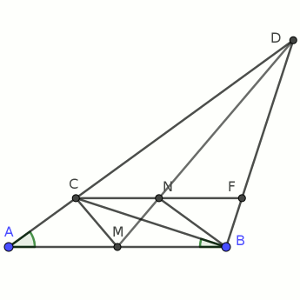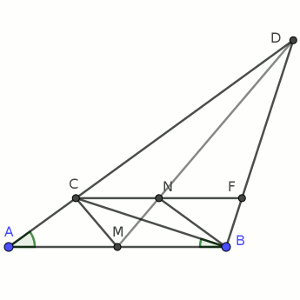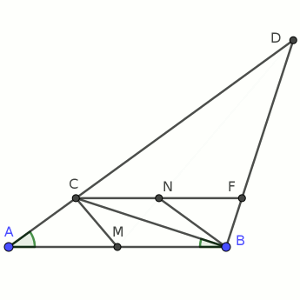
Puesto que el ángulo ACB forma un triángulo con el ángulo en B (que llamaremos b) y en A (2b), resulta que ACB = 180 – 3b, por lo que DCB es el ángulo 3b. Si descomponemos 3b = 2b + b, resulta que al trazar una línea paralela a AB, corta el ángulo DCB en uno de b y otro de 2b. Esa línea, que corta el segmento DB en el punto F, forma ángulos con DB DFC = 90 + b (igual que DBA) y CFB = 90 – b.
Pero si ahora trazamos un segmento que forme un ángulo b con BC, y que corte a CF en N, tenemos dos triángulos isósceles, BNF y BNC (ya que NBF va a medir 90 – b y NBC va a medir b). Eso significa que CN = NB = NF. Pero, claro, puesto que CN = NF, siendo CF una recta paralela a AB, el segmento DM pasa precisamente por N.
Y, por lo tanto, la figura que aparece con los puntos ACNBM es totalmente simétrica, un trapecio isósceles con su base mayor dividida en dos partes iguales, por lo que es evidente que los ángulos CMA y NMB (que coincide, claro, con DMB) son idénticos.