Problema 3 del nivel B de la Fase Comarcal de la de la XXX OMCV 2019
Se dirige a una edad de: 14-15 años

Encuentra una terna de enteros positivos x, y, z tales que se cumpla la siguiente igualdad:

97/19 = 5 + 1/(x + 1/(y + 1/z))

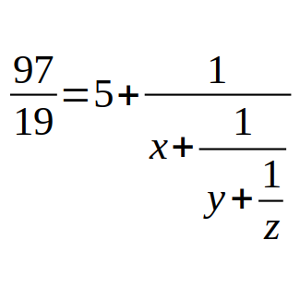
Solución:

La clave en esta igualdad (salvo que conozcas las fórmulas relativas a las fracciones continuas) es que en cada suma uno de los dos sumandos es menor o igual que 1, ya que x, y y z son mayores o iguales que 1.

Puesto que 97/19 es un número entre 5 y 6, calculamos 97/19 – 5 y será igual que la fracción, es decir, que 2/19 = 1/(x + 1/(y + 1/z)), por lo que, invirtiendo ambas fracciones, tenemos que 19/2 = x + 1/(y + 1/z).

De la misma forma, 19/2 es un número entre 9 y 10, por lo que x debe ser 9, y la diferencia entre 19/2 y 9, 19/2 – 9, será igual a la fracción. Tenemos, por tanto, que 1/2 = 1/(y + 1/z). De nuevo, invirtiendo ambas fracciones, tenemos que 2 = y + 1/z.

Por fin, como 1/z no puede ser nulo y sí puede valer 1, está claro que y = 1 y z = 1, porque no puede darse que y sea 2.

En resumen, x = 9, y = 1 y z =1.

No sería admitida como fracción continua estándar, ya que ninguna puede acabar en 1, sería equivalente a [5;9,2].