Problema 2 de la Fase Nacional de la de la LV OME 2019
Se dirige a una edad de: 16-17 años

Determinar si existe un conjunto finito S formado por números primos positivos de manera que para cada entero n ≥ 2, el número 2² + 3² + … + n² sea múltiplo de algún elemento de S.

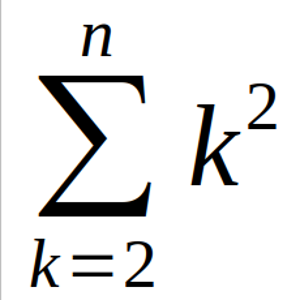
Solución:

Lo primero que debemos hacer es entender bien la pregunta. Lo que pide es saber si existe un conjunto de primos que garantice que todos los elementos de un conjunto infinito son múltiplos de alguno de los primos del conjunto.

Por ejemplo, si tomamos un conjunto que contenga a todos los pares y los múltiplos de 7 ({2, 4, 6, 7, 8, 10, 12, 14, …}), por ejemplo, existiría un conjunto de dos primos (evidentemente, {2,7}) para el que todos los elementos del conjunto infinito son múltiplos.

Sin embargo, si pensamos en el conjunto infinito de los impares, no hay tal conjunto finito, ya que existen infinitos primos impares, y cada vez que apareciera uno deberíamos añadirlo al conjunto para que existiese tal conjunto, porque un primo no es múltiplo de ningún otro primo.

Otra cosa que debemos entender es cómo es el conjunto infinito con el que debemos trabajar, es decir, ver si tiene una expresión que nos sea más manejable.

Al tratarse de una suma de cuadrados, puede expresarse como un polinomio de grado tres en función del número de sumandos. Veamos cómo podemos encontrar encontrar esa expresión.

La forma en la que yo comprendí este hecho, y aprendí a calcular el polinomio, se basa en el desarrollo del binomio de Newton.

Por ejemplo, puesto que (x – 1)³ = x³ – 3x² + 3x – 1, resulta que x³ – (x – 1)³ = 3x² – 3x + 1, es decir, que (x³)/3 – ((x – 1)³)/3 = x² – x + 1/3.

Ahora vamos a eliminar la parte de primer grado. Para lograrlo, pensemos que (x – 1)² = x² – 2x + 1, así que de forma parecida a lo anterior, (x²)/2 – ((x – 1)²)/2 = x – 1/2. Por lo tanto, (x³)/3 + (x²)/2 – [((x – 1)³)/3 + ((x – 1)²)/2] = x² – x + 1/3 + x – 1/2 = x² – 1/6.

Por último, eliminemos 1/6. Como x – (x – 1) = 1, x/6 – (x – 1)/6 = 1/6. Así que (x³)/3 + (x²)/2 + x/6 – [((x – 1)³)/3 + ((x – 1)²)/2 + (x – 1)/6] = x² – 1/6 + 1/6 = x².

Así que tenemos un polinomio, p(x) = (x³)/3 + (x²)/2 + x/6 = (2x³ + 3x² + x)/6 que cumple p(x) – p(x – 1) = x². Ahora, es fácil ajustar el término independiente de este polinomio para que en x = 2 nos proporcione el valor inicial 4. Puesto que p(2) = (16 + 12 + 2)/ 6 = 5, es suficiente restarle 1, y así tenemos el polinomio q(x) = p(x) – 1 = (2x³ + 3x² + x – 6)/6.

Veamos que éste es un polinomio de los que necesitamos. Como q(2) = 4 = 2², sabemos que para n = 3, se cumple que q(n – 1) = 2² + … + (n – 1)². Si suponemos que q(n – 1) = 2² + 3² + … + (n – 1)² para un valor determinado n, resulta que q(n) = q(n – 1) + n² = 2² + 3² + … + (n – 1)² + n², por lo que la fórmula se cumple para todo valor entero positivo n a partir de 2.

Por supuesto, hay otras maneras de construirlo. Incluso hay gente que se sabe de memoria las fórmulas de las sumas de cuadrados, de cubos, etcétera. Pero me gusta tener recursos para reconstruirlas.

A pesar de las fracciones, este polinomio siempre da valor entero, debido a que es una suma de enteros. Para estudiar sus factores primos, es mejor tenerlo factorizado.

Usando el método de Ruffini, rápidamente encontramos un factor (x – 1), así que la expresión queda q(x) = (x – 1)(2x² + 5x + 6)/6. El otro factor, el polinomio de segundo grado, no se puede factorizar con números reales, así que deberemos trabajar con él así.

Unas cuantas pruebas nos sugieren que no parece haber un patrón de primos sencillo, así que vamos a tratar de demostrar que no existe ese conjunto de primos.

Ahora, supongamos que tenemos un conjunto de primos que cumple el enunciado, y veamos cómo construir un valor n de forma que q(n) no sea divisible por ninguno de sus elementos, con lo que demostraremos que no existe tal conjunto.

En primer lugar, elegiremos el n de forma que el factor x – 1 simplifique el denominador, lo que facilitará mucho el cálculo. Para ello, pensemos que n – 1 = 6k, así que n = 6k + 1, para cualquier valor de k. Usando ese conjunto de valores, tendríamos q(6k – 1) = 6k(2(6k² + 12k + 1) + 5(6k + 1) + 6)/6 = 6k(12k² + 24k + 30k + 2 + 5 + 6)/6 = k(12k² + 54k + 13).

Es muy sencillo obtener un número que sea múltiplo de todos los primos del conjunto finito, sencillamente multiplicándolos. Si a ese número le sumamos uno, tenemos un número que no será múltiplo de ninguno de ellos, porque su resto es uno con cualquiera de los números primos del conjunto. Tomemos k ese resultado. Al dividir por cualquiera de ellos, entonces, da de resto uno, y q(k), por tanto, al dividirlo, tendrá un resto igual a 1(12·1² + 54·1 + 13) = 12 + 54 + 1 = 67, es decir, que si el 67 es uno de los números del conjunto, se nos estropea la demostración, así que vamos a trabajar un poco más para obtener un valor de k más apropiado.

Hay un teorema llamado teorema chino del resto, que garantiza que (siempre que los elementos de un conjunto finito sean primos dos a dos) podemos construir un valor de k cuyos restos al dividir por los primos del conjunto finito sean como nosotros queramos, en concreto, por ejemplo, podemos elegir que dé de resto 1, excepto con el 67, con el que dé de resto, por ejemplo, 2. En ese caso, al dividir entre cualquiera de los primos dará 67, luego no será múltiplo de ninguno de esos primos. Y al dividirlo entre 67, sin embargo, el resto dará 2·(12·4 + 54·2 + 13) = 2·(48 + 108 + 13) = 2·169 = 2·13², que claramente no es múltiplo de 67, por lo que la existencia de tal conjunto no es posible.

Si no conoces el teorema citado, la idea es multiplicar todos los primos, menos el 67 (en caso de estar presente este primo). Se estudia qué resto da al dividir entre 67, que evidentemente será diferente de cero. Al multiplicar este número por los valores entre 1 y 66, dará los 66 posibles restos, entre ellos 1. Elegimos este valor y multiplicamos, por lo que tenemos un número que da 0 con todos los primos del conjunto, y 1 con 67. Al sumarle 1, tenemos el número que queríamos.

Con esta construcción tendríamos un valor n para el que q(n) no sería múltiplo de ningún elemento del conjunto que teníamos, por lo que en efecto tal conjunto sería imposible.