Problema 2 del segundo nivel de la XXV Olimpiada de Mayo (2019) Se dirige a una edad de 14 años
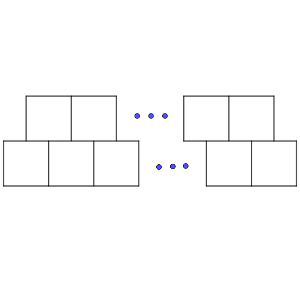
Se tiene un tablero con 2020 casillas en la fila inferior y 2019 en la superior, de forma que están ubicadas las casillas de una fila entre dos de la otra, como indica la figura.
En la fila inferior se colocan los números enteros del 1 al 2020 en algún orden.
Luego, en cada casilla superior se anota la multiplicación de los dos números que tiene debajo.
¿Cómo se pueden colocar los números de la fila inferior para que la suma de los números de la fila superior sea la menor posible?
Solución:
Ene este problema se requiere un alto nivel de intuición y razonamiento, difícil de encontrar a esta edad. De nuevo, vemos en la Olimpiada de Mayo una competición muy exigente, y es problable que este problema no obtuviese muchas puntuaciones máximas.
De nuevo vamos a intentar ver qué sucede con números más bajos. Si tratamos de ordenar los números del 1 al 6, buscando que las sumas de los productos consecutivos sea lo menor posible, veamos qué sucede.
1 – 2 – 3 – 4 – 5 – 6 los productos son 2 + 6 + 12 + 20 + 30. Si cambiamos 5 por 1, tenemos que queda 5 – 2 – 3 – 4 – 1 – 6, con lo que los productos son 10 + 6 + 12 + 4 + 6. Observamos que cambian 3 de los sumandos, no todos ellos a mejor. Sin embargo, la suma mejora. Si movemos cualquier pareja ahora, veremos que la suma aumenta.
Ahora bien, esto no basta para afirmar que es la mejor distribución, ya que tal vez podríamos encontrar una en la que moviendo varios a la vez, mejorara la suma de los productos. Una buena forma podría ser encontrar alguna propiedad que cumpliese ese orden y otro no, o bien ver que si un orden creemos que es el mejor, y podemos mejorarlo, claramente no lo es.
Está claro que hay otro orden, el inverso, en el que la suma de los productos da lo mismo (6 – 1 – 4 – 3 – 2 – 5). Imagina que hay otro orden en el que tenemos la suma óptima. Si en ese orden, el número más alto no está en un extremo, cambiarlo con el extremo produce una suma total menor.
Si lo hacemos con una cadena de 8 números, quedan así: 8 – 1 – 6 – 3 – 4 – 5 – 2 – 7.
Veámoslo con álgebra. Si el orden es x – a … y – 2020 – z …, y el 2020 no está en un extremo, al cambiarlo al extremo (2020 – a … y – x – z …) sólo cambia 3 valores, xa por 2020a, 2020y por xy, y 2020 por xz. Uno empeora (2020a – xa) = (2020 – x)a, mientras que hay dos que mejoran, ya que (2020 – x)y y (2020 – x)z, en total (2020 – x)(y + z). Claro, que esto depende de si la suma de y + z es menor o no que a. Probemos otra aproximación.
Imagina que tienes el orden x – a … y – 2020 – z …, y cambias al extremo el 2020, invirtiendo toda la cadena previa. De esta forma, todos los productos serán iguales menos uno, lo que nos permite compararlos. La cadena ahora será 2020 – y … a – x – z …, ahora la diferencia de una a otra es 2020z – zx, y como x es inferior, habremos salido ganando seguro.
Por tanto, la cadena óptima tiene el último valor en un extremo.
Veamos que el otro extremo debe estar ocupado por el segundo número en tamaño.
De forma similar a lo anterior, si la cadena es de la forma 2020 … x – 2019 – y … z, invertimos la cadena entre 2019 y el extremo, hasta que tenemos 2020 … x – z … y – 2019, todos los productos son iguales excepto uno, zx sustituye a 2019x, que es claramente mayor.
Ahora que está claro que los extremos están ocupados por los mayores números, en el problema 2020 y 2019, entre los demás busquemos qué orden nos interesa. En nuestro primer ejemplo, los menores números estaban junto a los mayores.
Si tenemos el orden 2020 – z … x – 1 – y … 2019, un orden supuestamente óptimo donde el z no es el 1, invirtiendo de nuevo la cadena z – … – 1, tenemos 2020 – 1 – x … z – y … 2019, en la que todo los productos son idénticos, excepto dos de ellos. 2020·z es reemplazado por 2020·1 y 1·y es reemplazado por z·y. En definitiva, la suma 2020·z + y es sustituida por 2020 + zy. Al restar el primer resultado menos el segundo, obtenemos 2020z – 2020 + y – zy = 2020(z – 1) + y(1 – z) = (z – 1)(2020 – y). Como ambos números son mayores que 0 (2020 es mayor que y y 1 es menor que z), tenemos que esa diferencia es mayor que 0, y por eso la suma total es menor. Luego en un orden óptimo, de nuevo 1 debe acompañar al 2020.
De forma similar, el 2 debe ir junto al 2019, ya que en ese caso se trata del menor número que queda. El razonamiento consiste en repetir la misma lógica y ver que de nuevo la diferencia es positiva.
Y junto al 1 y el 2, habrá que situar de nuevo, respectivamente, al 2018 y al 2017.
Así, conforme van quedando en el centro menos números, si los extremos son los más bajos, atraerán a los más altos, y si son los más altos, atraerán a los más bajos. Si repetimos el proceso, veremos que se va formando en un lado una progresión decreciente salteada de los pares mayores y los impares menores, y al revés en el otro lado. Curiosamente, al final quedan un par de sucesiones crecientes y decrecientes de pares e impares intercaladas.
Para hacerlo más de forma más técnica, a un nivel más alto, deberíamos probar por inducción que para una cadena de 2n valores diferentes, la cadena óptima tiene esa sucesión en los extremos, y para hacerlo se podría iniciar con los primeros, suponer que se cumple para los k mayores y los k menores, y ver que se cumple en el siguiente, razonando hacia el absurdo invirtiendo una cadena de valores para poder comparar sólo un par de sumandos.
En resumidas cuentas, la forma óptima de situar los números será:
2020 – 1 – 2018 – 3 … 1014 – 1009 – 1012 – 1011 – 1010 – 1013 … 4 – 2017 – 2 – 2019.