Problema 2 del nivel C de la Fase Provincial de la de la XXX OMCV 2019 Se dirige a una edad de: 10-11 años
En el pueblo quieren construir dos depósitos de agua (con tapa), y tienen que elegir entre dos proyectos que se han presentado.
El primero es un cilindro con radio 30,9 metros, y una altura de 50 metros.
El segundo es un depósito con forma de prisma rectangular, con una base de 30 por 100 metros, y una altura de 50 metros.
Calcula el volumen de cada proyecto, para encontrar cuál es el que tiene más capacidad.
Puesto que el material para hacerlo cuesta 3,2 € el metro cuadrado, ¿cuál sería el más barato de los dos al construirlo?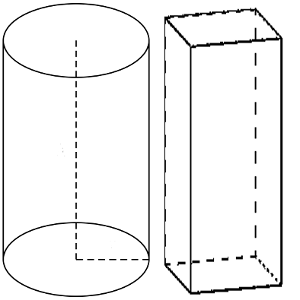
Solución:
No me acaban de gustar estos problemas, puesto que los que conocen las fórmulas obtienen una ventaja injusta. Es cierto que se pueden razonar, pero no es sencillo.
Ambos depósitos miden 50 metros de alto, y son rectos, por lo que su volumen coincidirá con el área de la base en metros cuadrados (que representa el número de cuadrados de un metro con los que podríamos recubrir su base) por 50 metros de alto, que serían las veces que los tendríamos que superponer para llenarlo.
En el caso del cilindro, será 30,9²·π·50, aproximadamente 149981 metros cúbicos, mientras que el segundo sería 30·100·50 = 150000 metros cúbicos. Por lo tanto, el segundo sería algo mayor, aunque poco más.
El material se puede calcular estudiando por separado la tapa y la base, y el material del lateral, que tiene que doblarse entorno al perímetro de la base.
En el primer caso, las dos tapas medirían 30,9²·π, mientras que el perímetro sería 30.9·2·π, que habría que rodear con un rectángulo de 50 metros de alto. En total 2·30,9²·π + 30.9·2·π·50 = 15707 metros cuadrados, aproximadamente.
En el segundo, las dos tapas miden 30·100, y el perímetro de la base mide 60 + 200 = 260 metros, por lo que el área total sería 2·30·100 + 260·50 = 19000 metros cuadrados.
Claramente, el segundo sale mucho más caro de fabricar. La diferencia sería de unos 3293·3,2 = 10537€.
No es extraño, ya que el círculo tiene una mejor relación entre perímetro y área que el cuadrado.