Problema 1 de la Olitele 2019
Se dirige a una edad de: 16-17 años

La figura muestra dos rectángulos, ABCD y BEFD, de forma que el lado DB del segundo rectángulo es una diagonal del primero y el lado EF pasa por C.

Si conocemos los lados m y p del primer rectángulo ¿Cuál es el área del segundo rectángulo?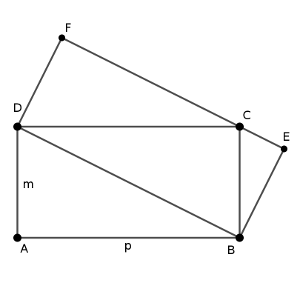
Solución:

El área es m·p, exactamente igual que el área del primero.

Se puede pensar rápidamente en que la parte común es la mitad en ambos rectángulos, ya que en un caso por simetría es evidente, y en otro es la unión de dos triángulos que comparten la altura, y en total tienen la base idéntica.

Es decir, que el área del triángulo rectángulo DBC es igual a la suma de las áreas de los triángulos BEC y DFC, ya que la altura es FD en todos los casos, y las bases FC y CE suman lo mismo que la base BC del otro.

También podemos tratar de calcular la longitud de la altura utilizando rectas, o cualquier otro medio geométrico, y saldrá que la altura de C sobre el lado DB es m·p/(raíz(p² + m²)), con lo que al multiplicarlo por la base, obtenemos el mismo resultado.

Por ejemplo, poniendo la figura en coordenadas, situando A en (0,0), D sería (0,m), B sería (p,0) y C sería (p,m).

Puesto que las componentes del vector DB son (p, -m), la ecuación de la recta DB sería mx + py = pm. Es decir, que la fórmula de distancias a esa recta sería |(mx + py – pm)/(raíz(p² + m²)|. Al sustituir el punto C, tenemos que da |(mp + pm – pm)/(raíz(p² + m²)| = m·p/(raíz(p² + m²)).

Y, por supuesto, el área sería m·p.