Problema 1 de la Fase Local de la LVI OME 2020 Se dirige a una edad de: 16-17 años
Dado un número natural n > 1 realizamos la siguiente operación: si n es par, lo dividimos entre 2; si n es impar, le sumamos 5.
Si el número obtenido tras esta operación es 1, paramos el proceso; en caso contrario, volvemos a aplicar la misma operación, y así sucesivamente.
Determinar todos los valores de n para los cuales este proceso es finito, es decir, se llega a 1 en algún momento.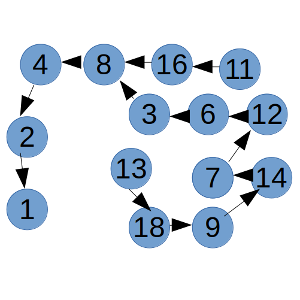
Solución:
Un problema bastante sencillo que tiene cierta relación con una de las conjeturas aún no probadas más famosas en matemática, la de Collatz, sobre la que se acababa de hacer un serio avance en las fechas en las que se convocó esta prueba.
Probando con los números más pequeños, generamos secuencias muy sencillas (2, 1), (3, 8, 4, 2, 1), (4, 2, 1), (5, 10, 5, …), (6, 3, 8, 4, 2, 1), (7, 12, 6, 3, 8, 4, 2, 1), (8, 4, 2, 1), (9, 14, 7, 12, 6, 3, 8, 4, 2, 1) y (10, 5, 10, …).
Rápidamente hacemos una conjetura: los múltiplos de 5 no pertenecen a este conjunto, mientras que los que no lo son sí que siguen un proceso finito.
Con esta respuesta daría para algún punto de los 7 que dan por el problema, pero hace falta probar dos afirmaciones de forma rigurosa para ganar todos los puntos: que los múltiplos de 5 generan un proceso no finito, y que los no múltiplos de 5 sí que generan un proceso finito.
Ver que los múltiplos de 5 generan un proceso infinito es sencillo, ya que tanto dividirlos entre 2 si son pares, como sumarles 5 si son impares genera otro múltiplo de 5, luego no pueden llegar nunca a 1, que no es múltiplo de 5, por lo que el proceso no se detiene.
Vayamos con los que no son múltiplo de 5. De la misma forma que para los múltiplos de 5 (y por las mismas razones), los números de la secuencia que generemos tampoco serán múltiplos de 5.
Supongamos que un número mayor de 6 (los menores está claro que lo cumplen) no es múltiplo de 5 y genera una secuencia no finita. En ese caso, tomemos n como el menor de tales números.
No puede ser par, ya que el siguiente de la secuencia genera también una secuencia infinita (la misma, de hecho), y es menor (y habíamos supuesto que era el menor).
Pero si es impar, el siguiente de la secuencia sería 5 + n, que es par, y al dividirlo entre 2 para generar el siguiente obtendríamos un número (5 + n)/2, que también genera una secuencia infinita. Veamos que este número (5 + n)/2 es menor que n. En efecto, si (5 + n)/2 >= n, entonces, 5 + n >= 2n, es decir, 5 >= 2n – n = n, es decir, n sería menor que 5, y sabemos que eso no es así, por lo que tampoco puede ser impar.
Un proceso similar se podría probar por inducción, siguiendo pasos muy parecidos.