Escalera de cuadrados
Problema 8 del concurso marató de problemes 2020 Se dirige a una edad de: 14-15 años
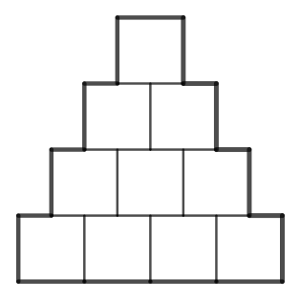
En la siguiente figura se aprecia una estructura de aspecto triangular hecha con cuadrados iguales, todos de lado 1 cm.
En la fila superior hay 1 cuadrado.
Bajo esa fila hay otra con dos cuadrados.
La tercera fila empezando desde arriba tiene tres cuadrados.
Y así sucesivamente, hasta la fila n, en la que hay n cuadrados.
La imagen corresponde a un n = 4.
Cada cuadrado recae sobre dos de los cuadrados de la fila previa, no necesariamente centrado, pero sin dejar huecos con los cuadrados vecinos.
Hay una línea negra dibujada que marca el polígono que rodea a todos estos cuadrados.
Indicamos con S la superficie de este polígono en cm² para un n determinado, y P al perímetro en cm del mismo polígono.
Se puede escribir S en función de P como un polinomio d segundo grado, independientemente del n. Esta relación se da para cualquier valor de n.
Encuentra los valores a, b, c que cumplen S = aP² + bP + c.
Solución: Aquí.
Solución a dos ortoedros unidos
Problema 7 del concurso marató de problemes 2020 Se dirige a una edad de: 14-15 años
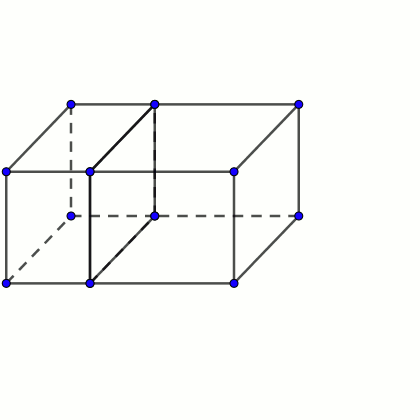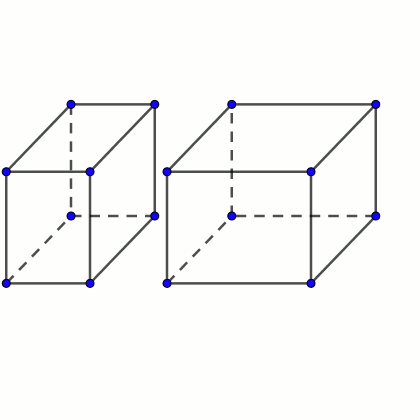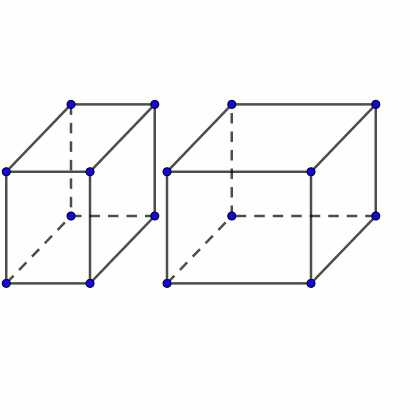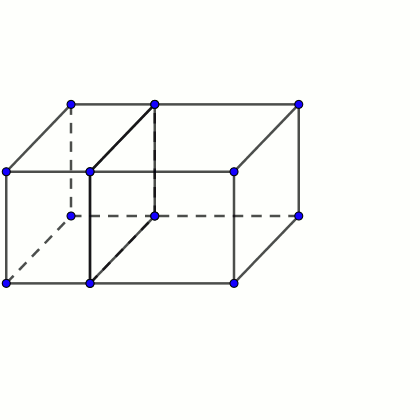
Un ortoedro es un poliedro con seis caras rectangulares perpendiculares cada una de ellas a sus vecinas.
Supongamos que tenemos dos octoedros que tienen la particularidad de que pueden unirse por una de sus caras para formar un ortoedro mayor.
Demuestra que, si la superficie total del ortoedro mayor es exactamente 3/4 de la suma de las superficies de los dos originales, entonces las dimensiones del ortoedro mayor x, y, z cumplen la relación 1/x + 1/y = 2/z.
Solución: (more…)
Dos ortoedros unidos
Problema 7 del concurso marató de problemes 2020 Se dirige a una edad de: 14-15 años
Un ortoedro es un poliedro con seis caras rectangulares perpendiculares cada una de ellas a sus vecinas.
Supongamos que tenemos dos octoedros que tienen la particularidad de que pueden unirse por una de sus caras para formar un ortoedro mayor.
Demuestra que, si la superficie total del ortoedro mayor es exactamente 3/4 de la suma de las superficies de los dos originales, entonces las dimensiones del ortoedro mayor x, y, z cumplen la relación 1/x + 1/y = 2/z.

Solución: Aquí.
Solución a un triminó atrapado
Problema 6 de la marató de problemes 2020 Se dirige a una edad de: 14-15 años
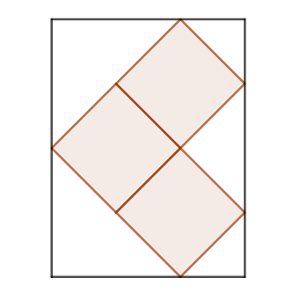
Se ha inscrito un triminó formado por tres cuadrados iguales unidos por sus lados formando un ángulo recto, en un rectángulo, de forma que cinco de sus vértices están en los lados del rectángulo, como se ve en la figura.
Si suponemos que el lado de cada cuadrado es un número conocido (pongamos que vale 3), calcula el área del rectángulo.
Solución: (more…)
Un triminó atrapado
Problema 6 de la marató de problemes 2020 Se dirige a una edad de: 14-15 años
Se ha inscrito un triminó formado por tres cuadrados iguales unidos por sus lados formando un ángulo recto, en un rectángulo, de forma que cinco de sus vértices están en los lados del rectángulo, como se ve en la figura.
Si suponemos que el lado de cada cuadrado es un número conocido (pongamos que vale 3), calcula el área del rectángulo.

Solución: Aquí.
Solución a un cuadrado con triángulos
Problema 1 de la I Math Home 2020 Se dirige a una edad de: 14-15 años
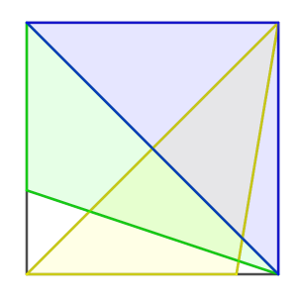
Dentro de un cuadrado de área 12 se colocan tres triángulos de áreas 4, 5 y 6, respectivamente.
Muestra que dos de los triángulos se solapan en una región de área mayor o igual a 1.
Solución:
En realidad, da igual que las formas que dibujes en el interior del cuadrado tengan formas de triangulo o cualquier otra, así como que el exterior sea un cuadrado o tenga otra forma, siempre que sean medibles.
Cada uno de los puntos del cuadrado cumple que, o bien no está en ninguno de los tres triángulos, o bien sí lo está. Si está dentro del primero, puede ser que esté en otro o no.
Así se llega con paciencia a que el área del cuadrado es igual al área exterior de los tres triángulos más la suma de los tres, menos la suma de las tres intersecciones, más la suma de la intersección de los tres.
Así, Denotando el cuadrado como D y A, B y C los triángulos, a(D) = a(D – A∪B∪C) + a(A) + a(B) + a(C) – a(A∩B) – a(B∩C) – a(A∩C) + a(A∩B∩C).
De esta forma, 12 = a(D – A∪B∪C) + 15 – a(A∩B) – a(B∩C) – a(A∩C) + a(A∩B∩C), por lo que se tiene que a(A∩B) + a(B∩C) + a(A∩C) = 3 + a(D – A∪B∪C) + a(A∩B∩C).
Por lo tanto, si las tres áreas propuestas son menores que 1, alguna de las otras dos debe ser negativa, lo cual es absurdo.
Un cuadrado con triángulos
Problema 1 de la I Math Home 2020 Se dirige a una edad de: 14-15 años
Dentro de un cuadrado de área 12 se colocan tres triángulos de áreas 4, 5 y 6, respectivamente.
Muestra que dos de los triángulos se solapan en una región de área mayor o igual a 1.

Solución: Aquí.
Solución a sala de cine
Problema 4 de la Marató de problemes 2020 Se dirige a una edad de: 14-15 años
Una sala de cine hace cuentas acerca de la asistencia de espectadores.
Los cinco días de diario, la media aritmética es de 1100 asistentes.
El sábado y el domingo, la sala está llena.
Si se tienen en cuenta todos los días de la semana, la media sube un 24% respecto a los días de diario.
¿Cuál es la capacidad de la sala?

Solución: (more…)