Problema 8 del concurso marató de problemes 2020 Se dirige a una edad de: 14-15 años
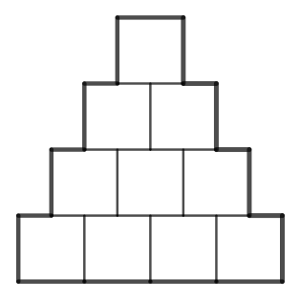
En la siguiente figura se aprecia una estructura de aspecto triangular hecha con cuadrados iguales, todos de lado 1 cm.
En la fila superior hay 1 cuadrado.
Bajo esa fila hay otra con dos cuadrados.
La tercera fila empezando desde arriba tiene tres cuadrados.
Y así sucesivamente, hasta la fila n, en la que hay n cuadrados.
La imagen corresponde a un n = 4.
Cada cuadrado recae sobre dos de los cuadrados de la fila previa, no necesariamente centrado, pero sin dejar huecos con los cuadrados vecinos.
Hay una línea negra dibujada que marca el polígono que rodea a todos estos cuadrados.
Indicamos con S la superficie de este polígono en cm² para un n determinado, y P al perímetro en cm del mismo polígono.
Se puede escribir S en función de P como un polinomio d segundo grado, independientemente del n. Esta relación se da para cualquier valor de n.
Encuentra los valores a, b, c que cumplen S = aP² + bP + c.
Solución:
Cada triángulo es una suma de una progresión aritmética, ya que cada fila tiene una más que la de arriba.
Como cada cuadrito tiene área 1, S = (1 + n)·n/2, para un número n de filas.
Es decir, que S = n/2 + n²/2.
Lo más difícil de ver es que el perímetro es 4n.
El lado de abajo claramente es n porque la última fila tiene n cuadrados.
El lado vertical de la derecha tiene n tramos de un centímetro, con lo que también mide n. Y lo mismo el de la izquierda.
Pero el horizontal superior tiene más tramos. El más de arriba tiene 1 cm, el siguiente nivel hay dos tramos que en total miden 1 cm, y así sucesivamente.
Si sumamos la parte superior de los n pisos, podemos ver fácilmente que mide también n cm.
Es decir, que P mide 4n, es decir, que n = P/4.
Como hay que sustituir en la fórmula, tenemos que S = P/8 + P²/32 (observa que n² = P²/16).
Por lo tanto S = (1/32)P² + (1/8)P + 0.
Por tanto lo que pide el problema es a = 1/32, b = 1/8, c =0.
Otra forma de solucionarlo es por una especie de “tanteo”.
Si probamos varios triángulos tenemos, por ejemplo, para la de 2 pisos, S = 3, P = 8.
Para la de 3 pisos, S = 6, P = 12.
Y para la de 4 pisos, S = 10, P = 16.
Entonces, poniendo todo junto, sabemos que 3 = 64a + 8b + c, 6 = 144a + 12 b + c y que 10 = 256a + 16b + c.
Cambiando los signos a la primera y restamos a las otras 2 para quedarnos sin c, tendríamos que:
3 = 80a + 4b
7 = 192a + 8b
Y, multiplicando la primera por -2 y sumando, tendríamos que 1 = 32a, con lo que claramente a = 1/32, b = 1/8 y c = 0.