Problema 6 de la marató de problemes 2020
Se dirige a una edad de: 14-15 años

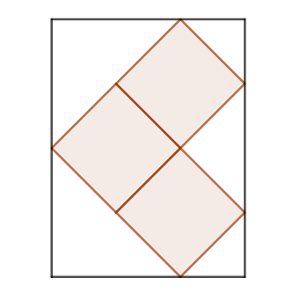
Se ha inscrito un triminó formado por tres cuadrados iguales unidos por sus lados formando un ángulo recto, en un rectángulo, de forma que cinco de sus vértices están en los lados del rectángulo, como se ve en la figura.

Si suponemos que el lado de cada cuadrado es un número conocido (pongamos que vale 3), calcula el área del rectángulo.

Solución:
Hay dos aproximaciones y ambas funcionan.

Una de ellas consiste en calcular la altura de los triángulos rectángulos que forma el rectángulo con los lados de los cuadrados. Tiene el inconveniente de que arrastras muchas raíces (aparece raíz(2) en muchas ocasiones), pero es sencillo calcular el área y se llega al resultado.

La otra es más difícil de ver de golpe, pero cuando lo hacemos no requiere ningún cálculo, consiste en completar el dibujo de la siguiente manera.

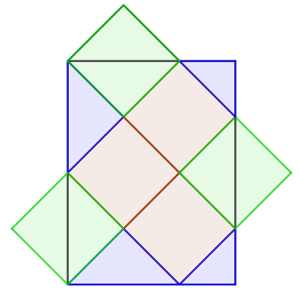
En ese caso, se ve que el área de los cuadrados verdes coincide con todo el espacio sobrante del rectángulo, ya que los trozos azules pueden superponerse sobre los trozos verdes que están por fuera del rectángulo. De esta forma, el área del rectángulo sería el doble de la pieza inicial.

Si ésta mide 3a², el rectángulo medirá 6a² (54 cm² en nuestro caso).