Problema 7 del concurso marató de problemes 2020
Se dirige a una edad de: 14-15 años

Un ortoedro es un poliedro con seis caras rectangulares perpendiculares cada una de ellas a sus vecinas.

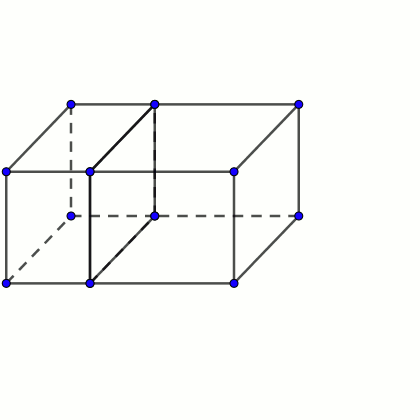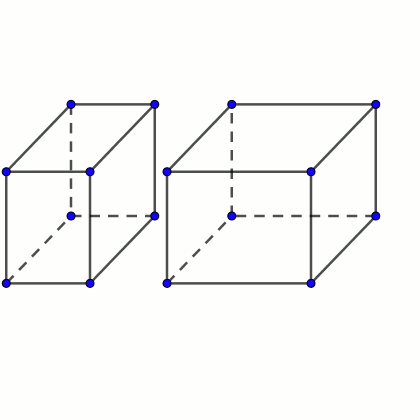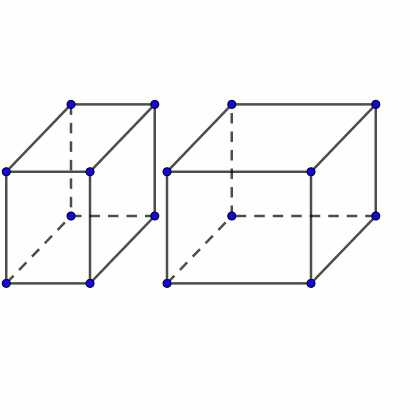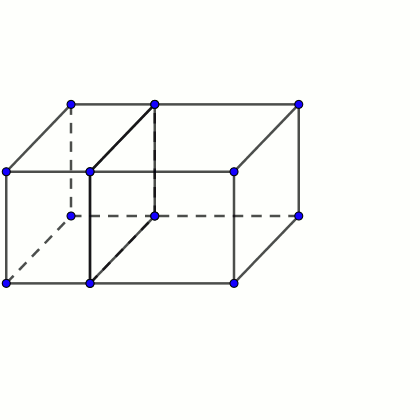
Supongamos que tenemos dos octoedros que tienen la particularidad de que pueden unirse por una de sus caras para formar un ortoedro mayor.

Demuestra que, si la superficie total del ortoedro mayor es exactamente 3/4 de la suma de las superficies de los dos originales, entonces las dimensiones del ortoedro mayor x, y, z cumplen la relación 1/x + 1/y = 2/z.

Solución:
Para poder simular el proceso, empecé a probar valores enteros que cumplieran la ecuación. Tras alguna prueba en la que daban decimales (también valen, pero es más pesado hacer los cálculos), encontré que si pones z =12, por ejemplo, 2/z = 1/6, de forma que puedes situar, por ejemplo, y = 18, y, restando, sale que x = 9. En efecto, 1/9 + 1/18 = 2/12. Parece que no, pero hay bastantes números enteros con los que jugar.

Probando con esta figura en concreto, me di cuenta de que bastaba en cortarla en dos por el lado de 12, es decir, dos ortoedros, por ejemplo, de 9, 18, 5 y 9, 18, 7. Pegándolos por la cara de 9×18 tenemos el efecto deseado.

Si te fijas, para calcular el área hay que multiplicar todas las longitudes por todas, y cada pareja sumarla dos veces. Pero como el lado que mide z es suma de los otros dos, cuando calculemos el área del grande muchas partes se podrán sumar.

Veamos cómo funciona con letras.

Tenemos dos ortoedros. Las dimensiones de uno son x, y, a. Las de otro, x, y, b. Ambos se pegan por una cara de dimensión x, y, formando un ortoedro de dimensiones x, y, z. Luego a + b = z.

El área del primero será 2xy + 2xa + 2ya y la del segundo 2xy + 2xb + 2yb. En total, las áreas de ambos serán 4xy + 2xa + 2xb + 2ya + 2yb, sacando factor común 4xy + 2xz + 2yz (recuerda que a + b = z).

Por otro lado, resulta que el área del ortoedro grande será 2xy + 2xz + 2yz. La diferencia será, por tanto 2xy.

Hay gente muy lista que se habrá dado cuenta antes: cuando pegas dos poliedros, el área es la suma de las áreas, menos la que pierdes cuando “tapas” las dos caras de unión, pero mucha gente es más lenta y necesita ejemplos.

Lo que dice el problema es que 2xy = (4xy + 2xz + 2yz)/4 (es decir, que en el proceso de pegado se pierde 1/4 del área, por eso después de unirlo el área total es 3/4 de la original).

Quitando denominadores, queda que 8xy = 4xy + 2xz + 2yz, es decir, que 4xy = 2xz + 2yz. Puesto que todo es par, podemos dividir por 2, y tenemos que 2xy = xz + yz.

Y la expresión original, si quitamos denominadores, da lo mismo, ya que 1/x + 1/y = 2/z es equivalente a xy/xyz + xz/xyz = 2xy/xyz. Con lo que queda demostrado.