Problema 11 del concurso marató de problemes 2020
Se dirige a una edad de: 14-15 años

Tenemos tres números relacionados, a, x e y, de forma que x = a + 1/a, y también y = a³ + 1/a³.

¿Puedes escribir una fórmula que permita expresar y en función de x?

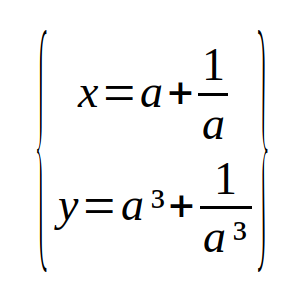
Solución:

Este problema tiene cierto truco.

Resulta que si queremos calcular x² en función de a, tenemos que es x² = (a + 1/a)² = a² + 2·a·1/a + (1/a)² = a² + 2 + 1/a².

Y si queremos calcular x³, será elevar al cubo la suma a + 1/a, que (bien porque hayamos hecho la multiplicación de (a + 1/a)² por a + 1/a, bien porque apliquemos la fórmula que permite elevar al cubo una suma) dará x³ = a³ + 3a²·(1/a) + 3a·(1/a)² + (1/a)³ = a³ + 3a + 3/a + 1/a³ = 3(a + 1/a) + y = 3x + y.

Por lo tanto, resulta que y = x³ – 3x.

Una manera directa, aunque mucho más larga de obtener lo mismo es despejar a en función de x y sustituir en la fórmula de y. Aunque también obtendríamos un resultado similar, el proceso puede llevar mucho más tiempo.

Puesto que x = a + 1/a, tenemos que ax = a² + 1, por lo que a² – ax + 1 = 0. Por lo tanto, a = (x ± raíz(x² – 4))/2, usando la fórmula de la ecuación de segundo grado.

Para poder calcular a³, podemos previamente calcular a². De esta forma, a² = (x² ± 2x·raíz(x² – 4) + x² – 4)/4 = (x² ± x·raíz(x² – 4) – 2)/2.

Ahora, para el cálculo de a³, podemos multiplicar a² por a (o aplicar la fórmula para el cubo de una suma), obteniendo que a³ = (x³ ± x²·raíz(x² – 4) – 2x ± x²·raíz(x² – 4) + x(x² – 4) ∓ 2raíz(x² – 4))/4 = (2x³ – 6x ± 2x²·raíz(x² – 4) ∓ 2raíz(x² – 4))/4 = (x³ – 3x ± x²·raíz(x² – 4) ∓ raíz(x² – 4))/2.

En esta expresión se puede sacar factor común la raíz, de forma que quedaría a³ = (x³ – 3x ± (x² – 1)raíz(x² – 4))/2.

Ahora, 1/a³ es la inversa, es decir, 2/(x³ – 3x ± (x² – 1)raíz(x² – 4)), pero para poder sumarlo deberemos racionalizarlo, obteniendo 2(x³ – 3x ∓ (x² – 1)raíz(x² – 4))/((x⁶ – 6x⁴ + 9x²) – (x⁴ – 2x² + 1)(x² – 4)) = 2(x³ – 3x ∓ (x² – 1)raíz(x² – 4))/((x⁶ – 6x⁴ + 9x²) – (x⁶ – 4x⁴ – 2x⁴ + 8x² +x² – 4)) = 2(x³ – 3x ∓ (x² – 1)raíz(x² – 4))/4 = (x³ – 3x ∓ (x² – 1)raíz(x² – 4))/2.

Cuando sumamos las dos expresiones, resulta que los factores que llevan raíz tienen signos contrarios, por lo que se anulan, y queda por tanto que y = a³ + 1/a³ = (x³ – 3x ± (x² – 1)raíz(x² – 4))/2 + (x³ – 3x ∓ (x² – 1)raíz(x² – 4))/2 = 2(x³ – 3x)/2 = x³ – 3x.

Como vemos, es un camino mucho más largo y confuso.